જળવાયુએ......... નું મિશ્રણ છે.
Easy
Download our app for free and get started
c
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બીજાઓથી નીચેના તફાવત સંયોજન $(3)$ વચ્ચે સૌથી યોગ્ય ઉદીપક કયો છે?View Solution
$(1)\,CH_3C \equiv C - CH_3$ $(2)\,CH_3CH_2 -CH_2 -CH_3$
$(3)\, CH_3CH_2C \equiv CH$ $(4)\, CH_3CH = CH_2$
- 2${C_2}{H_5}Cl$ની મહત્તમ નીપજ માટેની શરત કઈ છે?View Solution
- 3હાઇડ્રોલીસીસ પછી ઓઝોન સાથેની પ્રકિયા માટેના એકમાત્ર કાર્બનિક નીપજ તરીકે કયો આલ્કાઇન બ્યુટોનોઇક એસિડ $(CH_3 CH_2CH_2CO_2H)$ આપે છે?View Solution
- 4View Solutionનીચેની પ્રક્રિયાની મુખ્ય નીપજ કઈ હશે?
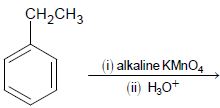
- 5$UV$ વિકિરણ ની હાજરીમાં પ્રોપિનની ડાયએઝો મિથેન સાથેની પ્રક્રિયાથી ........................ મળે છે.View Solution
- 6નીચે બતાવેલ $3,3$ - ડાયમિથાઇલ - $1$ -બ્યુટીન ના વધારાને ધ્યાનમાં લો.નિરીક્ષણ કરેલ નીપજ ની રચના માટે શ્રેષ્ઠ પદ્ધતિઓની સમજૂતી શું છે?View Solution
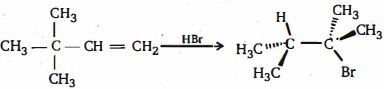
- 7$HBr$ તરફ ની પ્રતિક્રિયાશીલતાના ઘટતા ક્રમમાં ઉપરની ગોઠવણી કરોView Solution
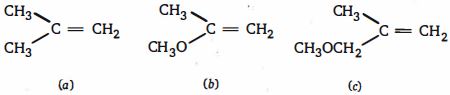
- 8View Solutionબેન્ઝિન......... પ્રક્રિયા દર્શાવે છે.
- 9નીચેની પ્રક્રિયામાં મુખ્ય નીપજ ($Y$) શું હશે ?View Solution
$\begin{array}{*{20}{c}}
{C{H_3}\,\,\,\,\,\,\,\,\,} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{C{H_3} - CH - C = CH}
\end{array}\xrightarrow[{{H_2}O}]{{HgS{O_4},{H_2}S{O_4}}}X$ $\xrightarrow[{(ii)\,conc.{H_2}S{O_4}/\Delta }]{{(i)\,{C_2}{H_5}MgBr,{H_2}O}}Y$ - 10$C{{H}_{3}}-C{{H}_{2}}-C{{H}_{2}}-C\equiv CH+\underset{\begin{smallmatrix}View Solution
Lithium\, \\
amide
\end{smallmatrix}}{\mathop{LiN{{H}_{2}}}}\,\to (A)\xrightarrow{{{(C{{H}_{3}})}_{2}}S{{O}_{4}}}(B)$નીપજ $(B)$ નું બંધારણ શું હશે ?