Hint: Here, we have to apply gauss's law to find electric charge.
Solution:
We know that, electric flux \(\phi_1\) (or electric field lines) entering in a closed
surface is -ve and electric flux \(\phi_2\) (or electric field lines) leaving a closed surface is \(+ve.\)
Hence, net electric flux through the closed surface,
\(\phi=\phi_2-\phi_1\)
Now, according to Gauss' theorem, the net electric flux \(\phi\) passing through a closed surface is equal to the \(1 / \varepsilon_0\) times of the total charge \(q\), inside the surface.
Step1: Apply gauss's law
Given, Net electric flux, \(\phi=\left(\phi_2-\phi_1\right)\)
\(\phi=\frac{ q _{\text {in }}}{\varepsilon_0}\)
\(\Rightarrow q_{\text {in }}=\varepsilon_0 \phi\)
\(\therefore q_{\text {in }}=\left(\phi_2-\phi_1\right) \varepsilon_0\)
Download our appand get started for free
Similar Questions
- 1બે પાતળી વિધુતભારિત સમતલ સપાટીની $\sigma_{+}$ પુષ્ઠ ધનતા અને $\sigma_{-}$ છે. જયા $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ બંને સમતલ લંબ છેદે છે. તો તંત્રની વિધુતક્ષેત્ર રેખાનું નિરૂપણView Solution
- 2નીચે બે વિધાન આપવામાં આવ્યા છે :View Solution
વિધાન $I :$ એક વિદ્યુત દ્વિધ્રુવીને પોલા ગોળાના કેન્દ્રમાં મૂકવામાં આવે છે. ગોળામાંથી પસાર થતા વિદ્યુત ક્ષેત્રનું ફલકસ શૂન્ય છે પરંતુ ગોળામાં ક્યાંય વિદ્યુત ક્ષેત્ર શૂન્ય નથી.
વિધાન $II :$ ઘન ધાત્વીક ગોળાની ત્રિજ્યા $'R'$ અને તેના પર રહેલો કુલ વિજભાર $Q$ છે.$r ( < R)$ ત્રિજ્યા ધરાવતા ગોલીય સપાટીના કોઈપણ બિંદુ પર વિદ્યુત ક્ષેત્ર શૂન્ય છે પરંતુ $‘r'$ ત્રિજ્યા ધરાવતા આ બંધ ગોલીય સપાટીમાંથી પસાર થતા વિદ્યુત ફ્લકસ નું મૂલ્ય શૂન્ય નથી.
ઉપરોક્ત વિધાનને અનુલક્ષીને આપેલ વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો :
- 3મુક્ત અવકાશમાં $z-$અક્ષ પર $8\, nC / m$ ના સમાંગ રેખીય વિદ્યુતભાર ધરાવતાં વિસ્તરમાં $x =3\, m$ બિંદુ આગળ વિદ્યુત ફલક્સ ઘનતા શોધો :View Solution
- 4આકૃતિમાં $A$ આગળના વિદ્યુતભાર પરનું બળ $BC$ ને લંબ દિશામાં ...... હશે.View Solution
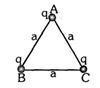
- 5દરેક $+q$ જેટલો વિદ્યાતભાર ધરાવતા બે નાના ગોળાઓ એક $2a$ લંબાઈની અવાહક દોરીથી જોડેલા છે તો દોરીમાં તણાવબળ કેટલું હશે?View Solution
- 6$Q$ અને $-Q$ વચ્ચેનું અંતર $d\, m$ છે.અને તેમની વચ્ચે લાગતું આકર્ષણ બળ $Fe$ છે.જયારે આ બંને વિદ્યુતભારને $0.3d$ ત્રિજયા ધરાવતા સમાન ગોળા પર મૂકવામાં આવે છે.કે જે બંને ગોળાના કેન્દ્ર વચ્ચેનું અંતર $d$ હોય,તો નવું આકર્ષણ બળView Solution
- 7View Solutionઘાતુના ગોળાને સમાન વિધુતક્ષેત્રમાં મૂકતા તેમાં વિધુતક્ષેત્ર રેખાનો સાચો માર્ગ કયો થાય?
- 8$10\,cm$ ત્રિજયા ધરાવતા સમાન રીતે વિદ્યુતભારીત અવાહક ગોળાથી $20\,cm$ અંતરે વિદ્યુતક્ષેત્ર $100\, V/m$ છે.તો કેન્દ્રથી $3 \,cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
- 9વિદ્યુતક્ષેત્ર ને $(6 \hat{i}+5 \hat{j}+3 \hat{k}) \mathrm{N} / \mathrm{C}$ વડે આપવામાં આવે છે. $YZ$ સમતલમાં રહેલા $30 \hat{i} \mathrm{~m}^2$ જેટલું ક્ષેત્રફળ ધરાવતી સપાટીમાંથી પસાર થતું વિદ્યુત ફલકસ $SI$ એકમમાં ________ થશે.View Solution
- 10$10 \,cm$ અને $15 \,cm$ ની બાજુઓ ધરાવતા લંબયોરસ પૃષ્ઠને એકરૂપ વિદ્યુતક્ષેત્ર $25 \,V / m$ માં એવી રીતે મૂકવામાં આવી છે કે જેથી પૃષ્ઠ વિદ્યુતક્ષેત્રની દિશા સાથે $30^{\circ}$ ખૂણો બનાવે તો આ લંબચોરસ પૃષ્ઠમાંથી વિદ્યુતક્ષેત્રનું ફલક્સ ................ $Nm ^2 / C$View Solution
