જ્યારે કોઈ ધાતુની સપાટી પર $\lambda$ તરંગલંબાઈનું વિકિરણ આપાત કરવામાં આવે ત્યારે તેનો સ્ટોપિંગ પોટેન્શિયલ $V$ મળે છે.જો સમાન સપાટી પર $3 \lambda$ તરંગલંબાઈનું વિકિરણ આપાત કરવામાં આવે ત્યારે તેનો સ્ટોપિંગ પોટેન્શિયલ $\frac{ V }{4}$ મળે છે. જો ધાતુની સપાટી ની થ્રેશોલ્ડ તરંગલંબાઈ $n \lambda$ હોય તો $n$ નું મૂલ્ય કેટલું હશે?
JEE MAIN 2020, Medium
a
\(\frac{ hc }{\lambda}=\frac{ hc }{\lambda_{0}}+ eV\)\(...(i)\)
\(\frac{ hc }{\lambda}=\frac{ hc }{\lambda_{0}}+ eV\)\(...(i)\)
\(\frac{ hc }{3 \lambda}=\frac{ hc }{\lambda_{0}}+\frac{ e \cdot V }{4}\)\(...(ii)\)
(multiply by \(4\))
\(\frac{4 hc }{3 \lambda}=\frac{4 hc }{\lambda_{0}}+ eV\)\(...(iii)\)
From \((i)\) \(\&\) \((iii)\)
\(\frac{h c}{\lambda}-\frac{h c}{\lambda_{0}}=\frac{4 h c}{3 \lambda}-\frac{4 h c}{\lambda_{0}}\)
\(-\frac{ hc }{3 \lambda}=-\frac{3 hc }{\lambda_{0}}\)
\(9 \lambda=\lambda_{0}\)
\(n=9\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ધાતુ સપાટી ઉપર $4500 \,\mathring A$ તરંગલંબાઈનું વિકિરણ આપાત કરવામાં આવે છે. ઉત્સર્જાયેલ ફોટો-ઈલેકટ્રોન $2 \,mT$ જેટલું અચળ યુંબકીય ક્ષેત્રમાં યુંબકીય ક્ષેત્ર સાથે $90^{\circ}$ ના કોણે દાખલ થાય છે. હવે તે જો $2 \,mm$ ના વત્તુળ ઉપર ભ્રમણ કરવાનું શરૂ કરે તો ધાતુનું કાર્યવિધેય લગભગ ......... $eV$ થશે.View Solution
- 2જ્યારે $hv$ ઊર્જાનો ફોટોન એલ્યુમિનિયમ ની પ્લેટ પર આપાત થાય (કાર્ય વિધેય $E_0$) ત્યારે મહત્તમ ગતિ ઊર્જા $K$ ધરાવતા ફોટો ઈલેક્ટ્રોન બહાર નીકળે છે. જ્યારે $2hv$ ઊર્જાનો ફોટોન એલ્યુમિનિયમ ની પ્લેટ પર આપાત થાય ત્યારે બહાર નીકળતાં ફોટો ઈલેક્ટ્રોનની મહત્તમ ગતિ ઊર્જા કેટલી હશે?View Solution
- 3એક $10\ kW$ ટ્રાન્સમીટર $500\ m$ તરંગ લંબાઈના રેડિયો તરંગને ઉત્સર્જન કરે છે. તો ટ્રાન્સમીટર વડે પ્રતિ સેકન્ડે ઉત્સર્જતા ફોટોનની સંખ્યા .....ક્રમની છે.View Solution
- 4ફોટો સંવેદી પદાર્થના પૃષ્ઠ પર $300\ nm$ અને તરંગ લંબાઈ અને $1.0 watt/m^2$ તીવ્રતાનો પારજાંબલી પ્રકાશ આપાત થાય છે. જો $1\%$ આપાત ફોટોન ફોટો ઈલેક્ટ્રોન ઉત્પન્ન કરે તો પૃષ્ઠના $1.0\ cm^2$ ક્ષેત્રફળમાંથી ઉત્સર્જાતા ફોટો ઈલેક્ટ્રોનની સંખ્યા ......છે.View Solution
- 5$\lambda$ તરંગલંબાઈવાળા ફોટોનની ઊર્જા $2\ eV$ છે તે ધાતુની સપાટી પર પડતાં ઉત્સર્જતા ફોટો ઈલેક્ટ્રોનનો મહત્તમ વેગ $v$ છે. જો $\lambda$ નું મૂલ્ય $25\%$ ઘટાડીએ અને મહત્તમ વેગ બમણો કરીએ તો ધાતુનું વર્કકંક્શન ...... $eV$ થાય.View Solution
- 6કાઇ નિશ્ચિત ધાતુમાં ફોટો ઈલેક્ટ્રિક અસર ઉત્પન કરી શકે તે માટે વિકિરણની મહત્તમ તરંગલંબાઈ $200 \;nm$ છે. $100\; nm$ તરંગલંબાઈનાં વિકિરણને કારણે ઈલેક્ટ્રોન દ્વારા પ્રાપ્ત થતી મહત્તમ ગતિઉર્જા કેટલી હશે?View Solution
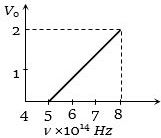
- 7ફોટોઇલેકટ્રોનનો સ્ટોપિંગ વોલ્ટેજ ${V_0}$ વિરુધ્ધ આપાત આવૃત્તિ $v$ નો આલેખ આપેલ છે.તો થ્રેશોલ્ડ તરંગલંબાઇ કેટલી થાય?View Solution
- 8એક ધાતુ સપાટી ઉપર $4500 \,\mathring A$ તરંગલંબાઈનું વિકિરણ આપાત કરવામાં આવે છે. ઉત્સર્જાયેલ ફોટો-ઈલેકટ્રોન $2 \,mT$ જેટલું અચળ યુંબકીય ક્ષેત્રમાં યુંબકીય ક્ષેત્ર સાથે $90^{\circ}$ ના કોણે દાખલ થાય છે. હવે તે જો $2 \,mm$ ના વત્તુળ ઉપર ભ્રમણ કરવાનું શરૂ કરે તો ધાતુનું કાર્યવિધેય લગભગ ......... $eV$ થશે.View Solution
- 9પ્રકાશના કિરણપુંજમાં $4972\,\mathop A\limits^o $ અને $6216\,\mathop A\limits^o $ તરંગલંબાઈ છે જેની કુલ તીવ્રતા $3 .6 \times 10^{- 3}\,\,Wm^{-2}$ છે જે બંને તરંગલંબાઈમાં સમાન રીતે વહેચાયેલ છે. આ કિરણપુંજ $1\,cm^2$ ની ધાતુની સપાટી જેનું વર્કફંકશન $ 2.3\,eV$ છે તેના પર લંબરીતે આપાત થાય છે. ધારો કે જ્યારે પ્રકાશનું પરાવર્તન થાય ત્યારે કોઈ પણ પ્રકારના પ્રકાશનો વ્યય થતો નથી અને દરેક સક્ષમ ફોટોન એક ઇલેક્ટ્રોનનું ઉત્સર્જન કરે છે. તો $2\,s$ માં કેટલા ફોટોઇલેક્ટ્રોનનું ઉત્સર્જન થયું હશે?View Solution
- 10$6.125\ eV$ નું વર્ક ફંકશન ધરાવતી ધાતુ પર $8 \times {10^{15}}\ Hz$ આવૃત્તિ આપાત કરતાં ફોટો- ઇલેકટ્રોનની ગતિઊર્જા કેટલા .......... $eV$ થાય?View Solution
