જ્યારે સાયકલો હેકઝેનને પાણીમાં નાખતા તે તરે છે કારણ કે.....
Diffcult
Download our app for free and get started
d
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેના સંયોજનો પૈકી એક, જે કેન્દ્રાનુરાગી નાઇટ્રેશન તરફ સૌથી વધુ ક્રિયાશીલ છે તે છે...
- 2હાઇડ્રોકાર્બનમાં $C_2, C_3, C_5$ અને $C_6$ સંકરણની અવસ્થા જણાવો,View Solution
$\begin{array}{*{20}{c}}
{C{H_3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C{H_3}\,\,\,\,\,\,\,} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\,\,\,\,\,\,\,\,\,\,\,\,} \\
{\mathop C\limits_7 {H_3} - \mathop C\limits_6 - \mathop C\limits_5 H = \mathop C\limits_4 H - \mathop C\limits_3 H - \mathop C\limits_2 \equiv \mathop C\limits_1 H} \\
{|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\
{C{H_3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}
\end{array}$જે નીચેના ક્રમમાં છે.
- 3$1$ મોલ બેન્ઝિનના ઊચા તાપમાન $Ni$ ઉદ્દીપકની હાજરીમાં $3$ મોલ $H_2$ વડે હાઇડ્રોજિનેશન દ્વારા મળતી નીપજ... છે.View Solution
- 4View Solutionનીચેની પ્રકિયામાંથી કઈ સંભવિત મુખ્ય નીપજ છે ?
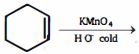
- 5View Solutionઉપરોક્ત ફ્રીડલ-ક્રાફ્ટ પ્રકિયા ની નીપજ કઈ છે ?
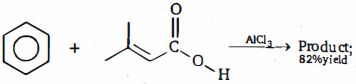
- 6ઈથાઈલ બેન્ઝિનનું $Cl_2$ સાથે મોનોક્લોરીનેશન કરવાથી ઉષ્મા ઉદભવતા શું મળે છે ?View Solution
- 7View Solutionનીચેના પરિવર્તન માટે સાચા પ્રક્રિયકનો સાચો ક્રમ શું છે?
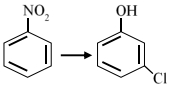
- 8આલ્કીન $(A)$ એ $H_2$ ના $3\, mole$ સાથે જોડાઈને પ્લેટિનમ ઉદીપક ની હાજરી માં $1$આઇસોપ્રોપાઇલ - $4$ -મિથાઇલ સાયકલોહેકઝેન બનાવે છે આલ્કીન એ આયોનાઈઝ અને ઘટે છે તો નીચેનામાંથી કઈ નીપજ મળશે ?View Solution
$\begin{matrix}
O \\
|| \\
H-C-H, \\
\end{matrix}\begin{matrix}
O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,O\,\,\,\,\,\,\,O\,\,\,\, \\
||\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,||\,\,\,\,\, \\
H-C-C{{H}_{2}}-C-C-C{{H}_{3}}, \\
\end{matrix}\begin{matrix}
\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,O \\
\,\,\,\,\,\,||\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|| \\
C{{H}_{3}}-C-C{{H}_{2}}-C-H \\
\end{matrix}$આલ્કેન$(A)$ શું હશે ?
- 9પ્રક્રીયામાંView Solution
$C{{H}_{3}}CH\,=\,\,C{{H}_{2}}\,+\,\,{{H}_{2}}O\,\,+\,\,[O]\,\,\underset{Acid}{\mathop{\xrightarrow{KMn{{O}_{4}}}}}\,$$\begin{array}{*{20}{c}}
{C{H_3} - CH - C{H_2}} \\
{\,\,\,\,\,\,\,\,\,|\,\,\,\,\,\,\,\,\,\,\,\,\,|} \\
{\,\,\,\,\,\,\,\,OH\,\,\,\,\,\,\,OH}
\end{array}$ $\xrightarrow{{[O]}}{\mkern 1mu} {\mkern 1mu} X{\mkern 1mu} {\mkern 1mu} + {\mkern 1mu} {\mkern 1mu} HCOOH$$X$ શું છે ?
- 10View Solutionનીચેનો કયો ઘટક બેન્ઝિન રિંગના સલ્ફોનેશનમાં ભાગ લે છે?