કિટો-ઇનોલ ચલરૂપકતા શેમાં જોવા મળે છે?
IIT 1988, Medium
Download our app for free and get started
d
(d) \(\mathop {{C_6}{H_5} - \mathop {\mathop C\limits^{||} }\limits^O - C{H_3}}\limits_{{\rm{(Keto}}\,{\rm{form)}}} \,{\rm{and}}\,\mathop {{C_6}{H_5} - \mathop {\mathop {C = }\limits^{|\,\,\,\,\,\,} }\limits^{OH} }\limits_{{\rm{(enol form)}}} C{H_2}\)
(d) \(\mathop {{C_6}{H_5} - \mathop {\mathop C\limits^{||} }\limits^O - C{H_3}}\limits_{{\rm{(Keto}}\,{\rm{form)}}} \,{\rm{and}}\,\mathop {{C_6}{H_5} - \mathop {\mathop {C = }\limits^{|\,\,\,\,\,\,} }\limits^{OH} }\limits_{{\rm{(enol form)}}} C{H_2}\)
\(\mathop {{C_6}{H_5} - \mathop {\mathop C\limits^{||} }\limits^O - C{H_2} - \mathop {\mathop C\limits^{||} }\limits^O - C{H_3}}\limits_{{\rm{(Keto form)}}} \,\)and
\(\mathop {{C_6}{H_5} - \mathop {\mathop C\limits_{||} }\limits_O - CH = \mathop {\mathop {C\,\,\,}\limits_{|\,\,\,\,} }\limits_{OH} - C{H_3}}\limits_{{\rm{(enol form)}}} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેના સંયોજનનું સાચું $IUPAC$ નામ જણાવો.View Solution
$\begin{array}{*{20}{c}}
{^{C{H_3}}} \\
{_H}
\end{array}\begin{array}{*{20}{c}}
{{\text{ }}\backslash {\text{ }}} \\
/
\end{array}\mathop C\limits^{} {\mkern 1mu} = \mathop C\limits^{} {\mkern 1mu} \begin{array}{*{20}{c}}
/ \\
{{\text{ }}\backslash {\text{ }}}
\end{array}_{\mathop C\limits^{} {\kern 1pt} \equiv \mathop C\limits^{} {\kern 1pt} - \mathop C\limits^{} {\kern 1pt} {H_2}\mathop C\limits^{} {\kern 1pt} {H_3}}^H{\mkern 1mu} $ - 2View Solutionસમધટકોના ........... સમાન હોય છે.
- 3સંયોજનો $A$ and $B$ ધરાવતું જલીય દ્રાવણ પ્રકાશ ક્રિયાશીલ પ્રવૃત્તિ બતાવે છે. $A$ અને $B$ અવકાશીય સમઘટક છે. નીચેની સંભાવનાઓ કઈ સાચી નથી હોતી?View Solution
- 4View Solutionનીચેનામાંથી કયા સંયોજનોની જોડી ઈનાસ્યોમેરિકની જોડી છે?
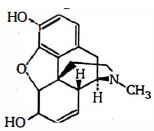
- 5મોર્ફિનમાં કેટલા કિરાલ કેન્દ્ર ($N$ કેન્દ્રોને બાદ કરતાં) છે.View Solution
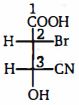
- 6View Solutionનીચેના પરમાણુમાં બે કેન્દ્રોના સંપૂર્ણ વિનયાસો કયા છે
- 7View Solutionપ્રતિબિંબકારક ....... દ્વારા ઓળખી શકાતાં નથી.
- 8View Solutionનીચેનામાંથી કોણ ભૌમિતિક સમઘટકતા દર્શાવે છે ?
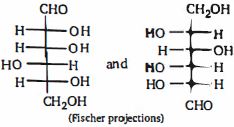
- 9View Solutionનીચેની કઈ જોડીમાં પરમાણુઓ વચ્ચે શું સંબંધ છે?
- 10View Solutionક્લોરોબ્યુટેનના તમામ પ્રકારના સમઘટકની સંખ્યા કેટલી છે