કોઈ એક ક્ષેત્રમાં સ્થિત વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્ર પ્રવર્તે છે.ચુંબકીયક્ષેત્ર $\vec B = {B_0}\left( {\hat i + 2\hat j - 4\hat k} \right)$ મુજબ આપવામાં આવે છે. જો એક વિજભાર આ ક્ષેત્રમાં $\vec v = {v_0}\left( {3\hat i - \hat j + 2\hat k} \right)$ ના વેગથી ગતિ કરતો હોય ત્યારે કોઈ બળ અનુભવતો ના હોય તો $SI$ એકમમાં વિદ્યુતક્ષેત્ર કેટલું હશે?
JEE MAIN 2017, Medium
d
According to question, as the test charge experiences no net force in that region i.e., sum of electric force \(\left( {{{\text{F}}_{\text{e}}} = {\text{q}}\overrightarrow {\text{E}} } \right)\,\) and magnetic forces \([{{\text{F}}_{\text{m}}} = {\text{q}}(\overline {\text{v}} \times \overline {\text{B}} ]\) will be zero.
According to question, as the test charge experiences no net force in that region i.e., sum of electric force \(\left( {{{\text{F}}_{\text{e}}} = {\text{q}}\overrightarrow {\text{E}} } \right)\,\) and magnetic forces \([{{\text{F}}_{\text{m}}} = {\text{q}}(\overline {\text{v}} \times \overline {\text{B}} ]\) will be zero.
Hence, \(F_{e}+F_{m}=0\)
\(\mathrm{F}_{\mathrm{e}}=-\mathrm{q}(\overline{\mathrm{v}} \times \overline{\mathrm{B}})\)
\(=-\mathrm{B}_{0} \mathrm{v}_{0}[(3 \hat{\mathrm{i}}-\hat{\mathrm{j}}+2 \hat{\mathrm{k}}) \times(\mathrm{i}+2 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})]\)
\(=-B_{0} v_{0}(14 \hat{j}+7 \hat{k})\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક બંધ વર્તુળાકાર લૂપનાં કેન્દ્ર સ્થાને (વિદ્યુતપ્રવાહ $i$ ધરાવતું લુપ) અલગ કરેલ ઉત્તર ધ્રુવ રહેલ છે. ઉત્તર ધ્રુવનાં કારણે વાયરનાં પરિઘ પર ચુંંબકીય ક્ષેત્ર $B$ છે. લુપની ત્રિજ્યા $a$ છે. આ વાયર પર બળView Solution
- 2$L$ બાજુવાળી સમક્ષિતિજ ચોરસ લૂપમાં $i$ પ્રવાહ પસાર થાય છે.હવે અડધી લૂપને વાળીને શિરોલંબ કરવામાં આવે છે. $ \overrightarrow {{\mu _1}} $ અને $ \overrightarrow {{\mu _2}} $ એ વાળ્યા પહેલા અને પછીની ચુંબકીય મોમેન્ટ હોય,તો નીચેનામાથી શું સાચું થાય?View Solution
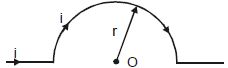
- 3તારને આકૃતિમુજબ $r$ ત્રિજયાના અર્ધવર્તુળમાં વાળતા કેન્દ્ર પર ચુંબકીયક્ષેત્ર .... .View Solution
- 4એક ચલિત ગૂંચળાવાળા ગેલ્વેનોમીટરમાં પ્રવાહ સંવેદિતા. $50 \%$ વધારવા માટે ગૂંચળામાં આંટાની સંખ્યા વધારવામાં આવે છે. ગેલ્વેનોમીટરની વોલ્ટેજ સંવેદિતામાં $..........\%$ પ્રતિશત ફેરફાર થશે.View Solution
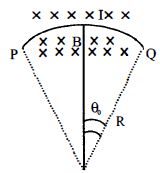
- 5ચુંબકીયક્ષેત્ર $B$ (કાગળના સમતલને લંબ $\times \times \times $ વડે દર્શાવેલ છે) માં એક તારને $R$ ત્રિજયા ધરાવતી ચાપ તરીકે $P$ અને $Q$ બિંદુ વચ્ચે જડિત કરેલ છે. જેમાંથી પ્રવાહ $I$ પસાર થાય છે. તો તારથી બનેલ ચાપ કેન્દ્ર સાથે $2\theta_0$ નો ખૂણો બનાવતી હોય તો તારમાં તણાવ કેટલું હશે?View Solution
- 6$90\, \Omega$ અવરોધ ધરાવતી કોઈલમાંથી પસાર થતો પ્રવાહ $90\%$ ઘટાડવા માટે ........... $\Omega$ મૂલ્યનો અવરોધ સમાંતરમાં જોડવો પડે?View Solution
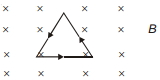
- 7એક તારને $100\,cm$ બાજુના સમભૂજ ત્રિકોણના સ્વરૂપમાં વાળવામાં આવ્યો છે અને $2\;A$ નો વિદ્યુતપ્રવાહ તેમાંથી વહે છે. તેને કાગળના સમતલની અંદર લંબ દિશામાં $2.0\,T$ પ્રેરણના ચુંબકીયક્ષેત્રમાં મૂકવામાં આવ્યો છે. ત્રિકોણની દરેક બાજુ પર લાગતા બળનું મૂલ્ય અને દિશા કેટલી હશે ?View Solution
- 8$4 \,cm$ ત્રિજયા અને $50$ આંટા ધરાવતી કોઇલમાં $2 \,A$ પ્રવાહ પસાર કરીને $0.1\, weber/{m^2} $ ના ચુંબકીયક્ષેત્રમાં મૂકેલી છે.સમતોલન સ્થિતિમાંથી $ 180^\circ $ ના ખૂણે ફેરવવા કેટલા .......$J$ કાર્ય કરવું પડે?View Solution
- 9$100\,V$ ના વિદ્યુતસ્થિતિમાનના તફાવત થી પ્રવેગિત કરેલ $2\,\mu\,C$ નો વિદ્યુતભાર $4\,mT$ તીવ્રતાના સમાન ચુંબકીયક્ષેત્રમાં ક્ષેત્રને લંબ દિશામાં દાખલ થાય છે. વિદ્યુતભારીત કણ ચુંબકીય ક્ષેત્રની અંદર $3\,cm$ ત્રિજ્યાનું અર્ધવર્તુળ પૂર્ણ કરે છે. વિદ્યુતભારીત કણનું દળ $........\times 10^{-18}\,kg$ હશે.View Solution
- 10$a$ ત્રિજ્યા ધરાવતો લાંબા સુરેખ તારના આડછેદ પર વિદ્યુતપ્રવાહ એકસમાન રીતે પથરાયેલ છે.તારની અક્ષથી $\frac{a}{3}$ અને $2 a$ અંતરે રહેલ ચુંબકીય ક્ષેત્રનો ગુણોત્તર કેટલો થાય?View Solution
