$L$ લંબાઈ અને $M$ દળનું એક દોરડું છત પરથી મુકત પાણે લટેકે છે. એક લંબગત તરંગને દોરડાના નિચેના છેડેથી ઉપર પહોંચતા લાગતો સમય $T$ છે, તો મધ્યબિંદુ સુધી તરંગને પહોંચતા લાગતો સમય કેટલો હોય.
Difficult
c
(c)
(c)
\(v=\sqrt{\frac{N}{\mu}}\)
The tension \(N\) in the string varies as :
\(N=\pi \frac{M g}{L} \times x\) where \(x\) is length from the ground.
\(d t=\frac{d x}{v_x} \text { and } v_x=\sqrt{\frac{M g x}{L \times M / L}}=\sqrt{g x}\)
\(\int \limits_0^T d t=\int \limits_0^L \frac{d x}{\sqrt{g x}}\)
\(T=\int \limits_0^L 2 \sqrt{x} d x\)
\(T=\int \limits_0^L 2 \sqrt{L_g} \quad \dots (i)\)
If time to cover half length is \(T_2\).
\(T_2=\sqrt{2 L g}\) [By putting limits \(0\) to \(L / 2\) in equation \((i)\)]
\(\frac{T}{\sqrt{2}}=T_2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થિર તરંગનું સમીકરણ $ y = 5\cos (\pi x/3)\sin 40\pi \,t \,cm$ હોય,તો બે નિસ્પંદ બિંદુ વચ્ચેનું અંતર કેટલું ... $cm$ થાય?View Solution
- 2$9\,Hz$ અને $11\,Hz$ આવૃતિ ધરાવતા બે તરંગના સંપાતીકરણથી તરંગનો ગ્રાફ કેવો મળે?View Solution
- 3હવામાં ધ્વનિની ઝડપ $330\, m/sec$ છે. હવામાં કોઈ વિશેષ ધ્વનિનો $40\;cm$ પથ તફાવત $1.6 \pi $ કળા તફાવતને બરાબર છે. આ તરંગની આવૃત્તિ ($Hz$ માં) કેટલી થાય?View Solution
- 4એક તરંગનું સમીકરણ $y = 7\sin \{ \pi (2t - 2x)\} $ મુજબ આપવામાં આવે છે જ્યાં $x$ મીટર અને $t$ સેકંડમાં છે. તો આ તરંગનો વેગ ($m/s$ માં) કેટલો હશે?View Solution
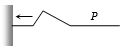
- 5આપાત તરંગ $P$ હોય,તો પરાવર્તિત તરંગ કેવું થાય?View Solution
- 6સોનોમીટરના તારની લંબાઈ $0.75\;m$ અને ઘનતા $9 \times 10^3\;Kg / m ^3$ છે. તે સ્થિતિસ્થાપક હદ ઓળંગવા સિવાય $8.1\times 10^8 \;N / m ^2$ નો તણાવ સહન કરી શકે છે. આ તારમાં ઉત્પન્ન કરી શકાતી મુળભુત આવૃતિ કેટલી હોય?View Solution
- 7$1$ મીટર લંબાઈનો તાર નિશ્ચિત પ્રારંભિક તણાવ હેઠળ $256 \,Hz$ મુળભુત આવૃતિનો અવાજ છોડે છે. જો તણાવ $1 \,kg$ વજનથી વધારવામાં આવે તો મુળભુત આવૃતિ $320 \,Hz$ થાય છે. તો પ્રારંભિક તણાવ ............... $kg \,wt$ હોય.View Solution
- 8View Solutionક્લોઝ પાઇપ (એક છેડેથી બંધ) ત્રીજા ઓવરટોનનું સમર્થન કરે છે. એવું જોવા મળે છે કે પાઈપમાં રહેલ હવા પાસે ...... હશે.
- 9View Solutionજ્યારે તાપમાન વધે, ત્યારે સ્વરકાંટાની આવૃત્તિ
- 10એક તરંગ સરળ આવર્ત ગતિ કરે છે તેનો આવર્ત $4 $ સેકન્ડનો છે જ્યારે અન્ય તરંગનો આવર્ત $3 $ સેકન્ડ છે. જો બંને તરંગો ભેગા થાય, તો આ પરિણામી તરંગનો આવર્ત કેટલો થાય?View Solution
