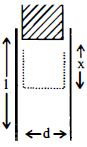
$l$ લંબાઈ અને $w$ જાડાઈ ધરાવતી પ્લેટમાંથી સમાંતર પ્લેટ કેપેસીટર બનાવવામાં આવે છે. જેમાં બે પ્લેટને એકબીજાથી $d$ અંતરે રાખવામા આવે છે. એક $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતો બ્લોક તેની વચ્ચે બરાબર ફિટ થાય તે રીતે પ્લેટની ધારની નજીક મૂકેલો છે. તેને કેપેસીટરની અંદર $F = -\frac{{\partial U}}{{\partial x}}$ જેટલા બળથી ખેચવામાં આવે છે, જ્યાં $U$ એ જ્યારે ડાઈઇલેક્ટ્રિક કેપેસીટરની અંદર $x$ અંતર જેટલો હોય ત્યારની કેપેસીટરની ઉર્જા છે. જો $Q$ એ કેપેસીટર પરનો વિજભાર હોય તો જ્યારે ડાઈઇલેક્ટ્રિક અચળાંકવાળો બ્લોક પ્લેટની ધારની નજીક હોય ત્યારે તેના પર કેટલું બળ લાગતું હશે?

JEE MAIN 2014, Diffcult
c
The electric force on the slab close to the edge is
The electric force on the slab close to the edge is
\(F=-\frac{\delta U}{\delta x}\)
The energy stored in the capacitor is
\(U=\frac{1}{2} \frac{Q^{2}}{C}\)
The capacitance in the case shown in the figure is
\(C = {C_1} + {C_2} = \frac{{{\varepsilon _0}wxK}}{d} + \frac{{{\varepsilon _0}w(l - x)}}{d}\)
\(=\varepsilon_{\circ} w \frac{x(K-1)+l}{d}\)
\(U=\frac{1}{2} \frac{Q^{2}}{C}\)
\(F=-(\delta U) /(\delta x)=-\frac{Q^{2} d}{2 \varepsilon_{\mathrm{o}} w} \frac{\delta}{\delta x}\left(\frac{1}{x(K-1)+l}\right)\)
\(F=\frac{Q^{2} d}{2 \varepsilon_{\mathrm{o}} w} \cdot \frac{K-1}{(x(K-1)+l)^{2}}\)
At \(x=0\) (edge):
\(F=\frac{Q^{2} d(K-1)}{2 \varepsilon_{0} w l^{2}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
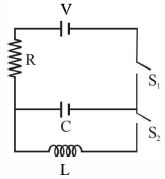
- 1નીચે દર્શાવેલ આકૃતિ મુજબ પ્રારંભમાં બંને કળ ખુલ્લી રાખેલ છે.હવે કળ $S1$ ને બંઘ કરવામાં આવે છે.પણ $S2$ ઓપન છે.( અત્રે કેપેસિટર પર $q$ ચાર્જ છે.$\tau $ $=RC$ કેપેસિટિવ અચળાંક છે.) નીચેના વિકલ્પો પૈકી કયું વિધાન સત્ય છે.?View Solution
- 2$1\,cm$ અને $2\, cm$ ત્રિજ્યા ધરાવતા બે ગોળાઓને $1.5 \times 10^{-8}$ અને $0.3 \times 10^{-7}$ કુલબના ધન વિદ્યુતભારથી વિદ્યુતભારીત કરેલા છે. જ્યારે તેઓને તાર વડે જોડવામાં આવે છે તો વિદ્યુતભાર......View Solution
- 3સમાન કેપેસિટન્સ $C$ ધરાવતાં કેપેસિટરને $V_1$ અને $V_2$ વોલ્ટેજથી ચાર્જ કરીને સમાંતરમાં જોડતાં તે કેટલી ઊર્જા ગુમાવશે?View Solution
- 4$12\, cm$ અને $9\, cm$ ત્રિજયા ધરાવતી ગોળીય કવચ વચ્ચે $6$ ડાઇઇલેકિટ્રક ધરાવતું માધ્યમ ભરવામાં આવે છે.બહારની ગોળીય કવચ ગ્રાઉન્ડ કરેલ છે,તો તંત્રનો કેપેસિટન્સ કેટલો થાય?View Solution
- 5એક કણ $A$ અનો વિદ્યુતભાર $+q$ અને $B$ નો વિદ્યુતભાર $+9\ q$ છે. પ્રત્યેક કણનું દળ $m$ સમાન છે. જો બંને કણોને સ્થિર સ્થિતિએથી સમાન સ્થિતિમાન તફાવત સાથે છોડવામાં આવે તો તેઓની ઝડપનો ગુણોત્તર ....... હશે.View Solution
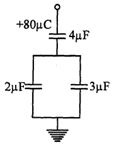
- 6આપેલ પરિપથમાં $4\ \mu F$ કેપેસિટરની ઉપરની પ્લેટને $+80\ \mu C$ કુલંબનો વિદ્યુતભાર આપવામાં આવે છે. તો સ્થિર સ્થિતિમાં $3\ \mu F$ કેપેસિટર ધરાવતા કેપેસિટરમાં ઉપરની પ્લેટનો વિદ્યુતભાર......$\mu C$View Solution
- 7View Solutionકોપર અને એલ્યુમિનિયમના સમાન વાહકને સમાન વિદ્યુતક્ષેત્રમાં મુકતા એલ્યુમિનિયમમાં પ્રેરિત થતો વિદ્યુતભાર ....
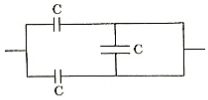
- 8View Solutionઆકૃતિમાં દર્શાવેલ સંયોજન માટે સમતુલ્ય સંધારકતા ..... છે.
- 9દસ વિદ્યુતભારને $R$ ત્રિજ્યાના વર્તુળ પર સમાન કોણીય અંતરે મૂકેલા છે. વિધુતભાર $1,3,5,7,9$ પાસે $(+q)$ અને વિધુતભાર $2,4,6,8,10$ પાસે $(-q)$ વિધુતભાર છે તો વર્તુળના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર અને વિદ્યુતસ્થિતિમાનView Solution
- 10$R$ ત્રિજ્યાવાળા ગોળાની સપાટી પર વિદ્યુતભાર $q$ સમાન રીતે વહેંચાયેલ છે. આ ગોળો, એક સમકેન્દ્રી પોલા ગોળાથી ઢંકાયેલ છે, જેની ત્રિજ્યા $2 R$ છે. જો બહારનો પોલો ગોલો પૃથ્વી સાથે જોડેલો હોય તો તેનાં પરનો વિદ્યુતભાર કેટલો હશે?View Solution
