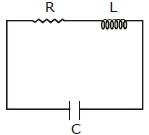
From \(kVL\) at any time :
\(\frac{q}{c}-i R-I \cdot \frac{d i}{d t}=0\)
\(\mathrm{i}=-\frac{\mathrm{d} q}{\mathrm{dt}} \Rightarrow \frac{\mathrm{q}}{\mathrm{c}}+\frac{\mathrm{dq}}{\mathrm{dt}} \mathrm{R}+\frac{\mathrm{Ld}^{2} \mathrm{q}}{\mathrm{dt}^{2}}=0\)
\(\frac{d^{2} q}{d t^{2}}+\frac{R}{I} \frac{d q}{d t}+\frac{q}{I c}=0\)
From damped harmonic oscillator, the amplitude is given by \(\mathrm{A}=\mathrm{A}_{0} \mathrm{e}-\frac{\mathrm{dt}}{2 \mathrm{m}}\)
Double differential equation \(\frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}+\frac{\mathrm{b}}{\mathrm{m}} \frac{\mathrm{dx}}{\mathrm{dt}}+\frac{\mathrm{k}}{\mathrm{m}} \mathrm{x}=0\)
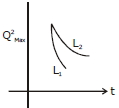
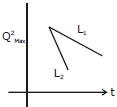
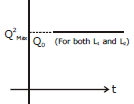
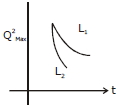
\(\mathrm{Q}_{\max }=\mathrm{Q}_{\mathrm{o}} \mathrm{e}-\frac{\mathrm{Rt}}{2 \mathrm{L}} \Rightarrow \mathrm{Q}_{\max }^{2}=\mathrm{Q}_{\mathrm{o}}^{2} \mathrm{e}-\frac{\mathrm{Rt}}{\mathrm{L}}\)
Hence damping will be faster for lesser self inductance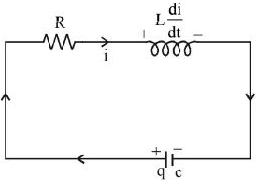
Download our appand get started for free
Similar Questions
- 1$L$ લંબાઇનો તાર છત પર બાંધેલ છે. બીજા છેડા પર $k$ બળઅચળાંક ઘરાવતી સ્પ્રિંગ સાથે બાંધેલ છે. $m$ દળનો પદાર્થ સ્પ્રિંગ સાથે બાંધેલ છે.તારનો આડછેદ $A$ અને યંગમોડયુલસ $Y$ છે. $m$ દળને ખેંચીને મૂકત કરતા સરળ આવર્તગતિનો આવર્તકાળ કેટલો થાય?View Solution
- 2એક કણ $A$ કંપવિસ્તાર સાથે સરળ આવર્ત ગતિ કરે છે. જયારે આ કણનું સ્થાનાંતર $\frac{2 A}{3}$ હોય ત્યારે તેની ઝડપ ત્રણ ગણી કરી દેવામાં આવે તો આ કણનો નવો કંપવિસ્તાર $\frac{\mathrm{nA}}{3}$ થઈ જ્તો હોય તો $\mathrm{n}=$.........View Solution
- 3સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $a $ અને આવર્તકાળ $3\, sec$ છે.સમતોલન બિંદુથી અડધા કંપવિસ્તાર સુધી પહોંચવા માટે કેટલો સમય ..... $\sec$ લાગે?View Solution
- 4એક કણ $A$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે.કણ જયારે તેની સરેરાશ અવસ્થાની $\frac{{2A}}{3}$ જેટલા અંતરે હોય છે,ત્યારે અચાનક તેની ઝડપ ત્રણ ગણી કરી દેવામાં આવે છે.કણનો નવો કંપવિસ્તાર છે:View Solution
- 5સમક્ષિતિજ દિશામાં $a$ પ્રવેગથી જતી ટ્રોલીમાં સાદા લોલકને લટકાવેલ હોય, તો આવર્તકાળ $T = 2\pi \sqrt {\frac{l}{{g'}}} $ મુજબ આપવામાં આવે, જ્યાં $g'$ કોને બરાબર થાય?View Solution
- 6View Solutionપ્રણોદિત દોલનોના કિસ્સામાં અનુનાદ તરંગ તીક્ષ્ણ બને જ્યારે .....
- 7એક પર્યાપ્ત ઉંચાઇના મકાનની છત પરથી એક લોલક લટકાવેલ છે, જે સાદા આવર્ત દોલકની જેમ મુક્તતાથી આગળ-પાછળ ગતિ કરી શકે છે. તેના સમતોલન સ્થાનથી $5\;m$ અંતરે આ લોલકનો પ્રવેગ $20\; m/s^2 $ છે. આ દોલનનો આવર્તકાળ કેટલો થાય?View Solution
- 8સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $x = 4(cos\pi t + sin\pi t)$ હોય, તો કંપવિસ્તાર કેટલો થાય?View Solution
- 9જ્યારે સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા દોલન દરમિયાન તેના મહત્તમ મૂલ્યના ચોથા ભાગની થાય, ત્યારે સમતોલન સ્થાનથી સ્થાનાંતર તેના કંપવિસ્તાર $a$ ના પદમાં કેટલું હશે?View Solution
- 10જ્યારે કણ સ.આ.ગ. કરે તો વેગનો સ્થાનાંતરના વિધેય તરીકેનો આલેખ $.....$ હશે.View Solution