$m $ દળના સાદા લોલક સાથે $m$ દળ અને $v_0$ વેગથી ગતિ કરતો કણ ચોંટી જાય છે.તો ગોળો કેટલી મહત્તમ ઊંચાઇ પ્રાપ્ત કરશે?
Diffcult
a
(a)Initial momentum of particle = \(m{V_0}\) Final momentum of system (particle + pendulum) \(= 2mv\) By the law of conservation of momentum
(a)Initial momentum of particle = \(m{V_0}\) Final momentum of system (particle + pendulum) \(= 2mv\) By the law of conservation of momentum
\(⇒\) \(m{V_0} = 2mv\)
\(⇒\) Initial velocity of system \(v = \frac{{{V_0}}}{2}\)
Initial K.E. of the system = \(\frac{1}{2}(2m){v^2}\)=\(\frac{1}{2}(2m){\left( {\frac{{{V_0}}}{2}} \right)^2}\)
If the system rises up to height \(h\) then \(P.E. =2mgh\)
By the law of conservation of energy \(\frac{1}{2}(2m){\left( {\frac{{{V_0}}}{2}} \right)^2} = 2mgh\)
\(⇒\) \(h = \frac{{V_0^2}}{{8g}}\)
= \(\frac{1}{2}(2m){\left( {\frac{{{V_0}}}{2}} \right)^2}\)
If the system rises up to height h then \(P.E. = 2mgh\)
By the law of conservation of energy
\(\frac{1}{2}(2m){\left( {\frac{{{V_0}}}{2}} \right)^2} = 2mgh\)
\(⇒\) \(h = \frac{{V_0^2}}{{8g}}\)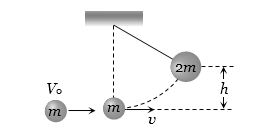
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક દડો જમીન પર અથડાઇને અસ્થિતિસ્થાપક સંઘાત બાદ ઉછળે છે. આ કિસ્સામાં.....
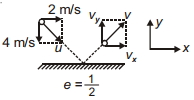
- 2$u$ ઝડપે લીસી અને સમક્ષિતિજ સપાટી સાથે ત્રાંસી અથડામણ અનુભવે છે. જેના $x$ અને $y$ ઘટકો દર્શાવેલ છે. જો રેસ્ટિટ્યુશન ગુણાંક $\frac{1}{2}$ હોય, તો અથડામણ પછીના $x$ અને $y$ ના ઘટકો $v_x$ અને $v_y$ અનુક્રમે ...... હશે ?View Solution
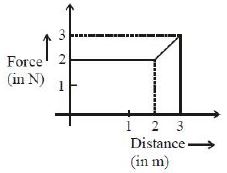
- 3ગ્રાફમાં દર્શાવ્યા પ્રમાણે એક કણ આપેલ સ્થાન સાથે બદલાતા બળના કારણે એક પારિમાણિક ગતિ કરે છે. $3\, m$ ગતિ કર્યા પછી કણની ગતિઉર્જા કેટલા .............. $\mathrm{J}$ થશે?View Solution
- 4$\mathrm{m}$ દળના કણને જમીનથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે.તે જ સમયે બીજા સમાન દળના કણને જમીન પરથી ઉપર તરફ $\sqrt{2 \mathrm{gh}}$ ના વેગથી ફેકવામાં આવે છે.જો બંને વચ્ચે અસ્થિતિસ્થાપક અથડામણ થતી હોય તો બંને ભેગા દળને જમીન પર આવતા $\sqrt{\frac{\mathrm{h}}{\mathrm{g}}}$ ના ગુણકમા કેટલો સમય લાગશે?View Solution
- 5એક સ્થિર કણ $m_1$ અને $m_2$ દળવાળા બે કણોમાં વિસ્ફોટ પામીને તે વિરુદ્વ દિશામાં $v_1$ અને $v_2$ જેટલા વેગથી ગતિ કરે છે. તેમની ગતિઊર્જાનો ગુણોત્તર ${E_1}/{E_2}$ કેટલો થાય?View Solution
- 6$0.5 kg$ ના દડાને $14 m/s$ ના વેગથી ઉપર તરફ ફેંકતા $8 m$ ઊંચાઇ પર જાય છે.દડો ઉપર જાય તે દરમિયાન હવા દ્વારા કેટલા ........... $J$ ઊર્જાનો વ્યય થશે?View Solution
- 7ટર્બાઈનનું સંચાલન કરવા $60\, m$ ઊંચાઈએથી અને $15\, kg/s$ ના દર થી પાણી પડે છે. ઘર્ષણ બળને કારણે થતો વ્યય આપાત ઊર્જના $10\,\%$ જેટલો છે. ટર્બાઈનમાં કેટલો પાવર (કાર્યત્વરા) ઉત્પન્ન થશે ? $\left(g=10\, \mathrm{~m} / \mathrm{s}^{2}\right)$ ($\mathrm{~kW}$ માં)View Solution
- 8કણની સ્થિતિઊર્જા $U = A - B{x^2} $ છે.તો કણ પર લાગતું બળView Solution
- 9$5\;m$ ઊંચાઈ પરથી રબરના દડાને મુક્ત કરવામાં આવે છે. તે જમીન સાથે અથડાઈનેતે તે જે ઊંચાઈથી પડે ત્યાથી તે દર ફેરે $\frac{81}{100}$ જેટલી ઊંચાઈ પ્રાપ્ત કરે છે, તો તેની આ ગતિ દરમિયાન સરેરાશ વેગ ($ms ^{-1}$ માં) કેટલો થાય?($g =10 ms ^{-2}$ )View Solution
- 10$0.25 Hp$ ની મોટર $600 rpm$ ની ઝડપથી ભ્રમણ કરે છે.જો કાર્યક્ષમતા $40\%$ હોય,તો એક પરિભ્રમણ પૂર્ણ કરતાં કેટલું કાર્ય થશે?View Solution
