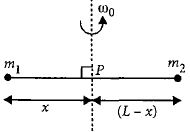
Moment of inertia of the system about the axis of rotation (through point \(P\)) is
\(I = {m_1}{x^2} + {m_2}{\left( {L - x} \right)^2}\)
By work energy theorem,
Work done to set the rod rotating with angular
velocity \({{\omega _0}}\) = Increase in rotational kinetic energy
\(W = \frac{1}{2}I\omega _0^2 = \frac{1}{2}\left[ {{m_1}{x^2} + {m_2}{{\left( {L - x} \right)}^2}} \right]\omega _0^2\)
For \(W\) to be mimimum,\(\frac{{dW}}{{dx}} = 0\)
\(i.e.,\,\frac{1}{2}\left[ {2{m_1}x + 2{m_2}\left( {L - x} \right)\left( { - 1} \right)} \right]\omega _0^2 = 0\)
or \({m_1}x - {m_2}\left( {L - x} \right) = 0 ( {{\omega _0} \ne 0}\)
or \({{m_1} + {m_2}} x = {m_2}L\,or\,x = \frac{{{m_2}L}} {{{m_1} + {m_2}}}\)
Download our appand get started for free
Similar Questions
- 1$L$ લંબાઈ અને $M$ દળ ધરાવતો એક પાતળો સળિયો તેને લંબ અને તેના કેન્દ્રમાથી પસર થતી અક્ષને અનુલક્ષીને ${\omega _0}$ ના અચળ કોણીય ઝડપથી ભ્રમણ કરે છે.બે $m$ દળ અને નહિવત પરિમાણ ધરાવતા મણકા શરૂઆતમાં સળિયાના કેન્દ્ર પર છે,જે સળિયા પર મુક્ત રીતે ભ્રમણ કરી શકે છે. જ્યારે મણકા સળિયાના છેડા પર હોય ત્યારે તંત્રની કોણીય ઝડપ કેટલી થશે?View Solution
- 2$30^o $ ના ખૂણાવાળા ઢાળ પર પોલો નળાકાર મૂકતાં $10\ m$ અંતર કાપ્યા પછી તેનો વેગ.......... $m/s$View Solution
- 3$V _{ CM }=2\; m / s , m =2\;kg , R =4 \;m$ જ્યારે રીંગ સંપૂર્ણ ગબડે ત્યારે તેનું કોણીય વેગમાન ઉદગમબિંદુને અનુલક્ષીને ($kgm ^{2} / s$ માં)View Solution
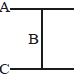
- 4નીચે આકૃતિમાં ત્રણ સમાન લંબાઈ અને સમાન દળ $M$ ધરાવતા સળિયા દર્શાવેલા છે. સળિયા $B$ ને આધાર રાખીને તંત્રને ભ્રમણ કરવવામાં આવે છે. તો આ તંત્રની જડત્વની ચાકમાત્રા શું થશે?View Solution
- 5ચાકગતિ કરતા બે પદાર્થનું કોણીય વેગમાન સમાન છે પરંતુ તેમની જડત્વની ચાકમાત્રા અનુક્રમે $I_1$ અને $I_2$ છે. ($I_1$ > $I_2$) કયા પદાર્થની ગતિ ઊર્જા વધુ હશે ?View Solution
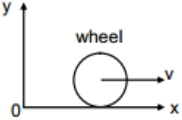
- 6$400\ Nm$ નું અચળ બળ યુગ્મ $100\ kg - m^2$ જડત્વની ચાકમાત્રા ધરાવતી વ્હીલને તેના કેન્દ્રમાંથી પસાર થતી અક્ષ પર ચાકગતિ કરાવે છે. $4\ s$ મેળવેલી કોણીય વેગ ....... $rad \,s^{-1}$ થશે .View Solution
- 7$R$ ત્રિજયા અને $R\over 6 $ જાડાઇ ઘરાવતી તકતીની જડત્વની ચાકમાત્રા $I$ છે. તેને પીગળાવીને ગોળો બનાવવામાં આવે તો ગોળાની જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 8એક $M$ દળની અને $R$ ત્રિન્યા વાળી વર્તુળાકાર તક્તિ સમક્ષિતિજ સમતલમાં તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ, $\omega$ કોણીય વેગથી ભ્રમણ કરે છે. જો સમાન પરિમાણ પરંતુ $\mathrm{M} / 2$ દળની બીજી તક્તિને પ્રથમ તક્તિ પબ સમાક્ષી રીતે હળવેકથી મૂકવામાં આવે તો તંત્રનો નવો કોણીય વેગ. . . . . . .છે.View Solution
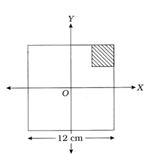
- 9આકૃતિમાં દર્શાવેલ $12\ cm$ લંબાઈની ચોરસ તકતીના એક ખૂણા પરથી $2\ cm $ લંબાઈનો એક ચોરસ કાપી લેવામાં આવે તો બાકી રહેતા ભાગનું દ્રવ્યમાન-કેન્દ્ર, મૂળ ચોરસના કેન્દ્રના સંદર્ભમાં કયાં હશે ? તકતી નિયમિત જાડાઈ અને ઘનતાની છે.View Solution
- 10આ પ્રશ્ન માં વિધાન $1$ અને વિધાન $2$ છે. આપેલ ચાર વિકલ્પોમાથી બંધબેસતો વિકલ્પ પસંદ કરો.View Solution
વિધાન $1$: જો પોતાની અક્ષને અનુલક્ષીને કોણીય ઝડપ $\omega $ થી ભ્રમણ કરતાં પદાર્થની જડત્વની ચાકમાત્રામાં વધારો થાય તો તેના કોણીય વેગ $L$ માં કોઈ પણ ફેરફાર નહિ થાય પણ જો ટોર્ક લગાવેલ નહિ હોય તો ગતિઉર્જા $K$ વધશે.
વિધાન $2$: $L = I\omega $, ભ્રમણ ની ગતિઉર્જા $ = \frac{1}{2}\,I\omega ^2$
