$n_{1}$ વક્રીભવનાંક ધરાવતા એક પ્રિઝમને $n_{2}$ વક્રીભવનાંક ધરાવતા બીજા પ્રિઝમ સાથે (આકૃતિમાં દર્શાવ્યા મુજબ) ચોટાડવામાં આવ્યા છે. $n_{1}$ અને $n_{2}$ એ $\lambda$ પર નીચે આપેલ સૂત્ર મુજબ આધાર રાખે છે, જ્યાં $\lambda$ એ પ્રકાશની તરંગલંબાઈ છે.
${n}_{1}=1.2+\frac{10.8 \times 10^{-14}}{\lambda^{2}}$ અને ${n}_{2}=1.45+\frac{1.8 \times 10^{-14}}{\lambda^{2}}$
$BC$ આંતરપૃષ્ઠ ઉપર કોઈ પણ ખૂણે આપાત કિરણ કે જે આંતર પૃષ્ઠ આગળ વાંકું વળ્યા વગર પસાર થઈ જાય તે તરંગલંબાઈ $....\,nm$ હશે.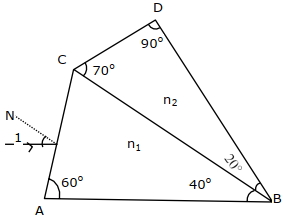
JEE MAIN 2021, Diffcult
Download our app for free and get started
b
For no deviation, \(n_{1}=n_{2}\)
For no deviation, \(n_{1}=n_{2}\)
\(1.2+\frac{10.8 \times 10^{-14}}{\lambda^{2}} =1.45+\frac{1.8 \times 10^{-14}}{\lambda^{2}}\)
\(0.25 =\frac{9 \times 10^{-14}}{\lambda^{2}}\)
\(\lambda^{2} =\frac{9 \times 10^{-14}}{0.25}\)
\(\lambda =\frac{3}{5} \times 10^{-6}\)
\(\lambda =6 \times 10^{-7} m\)
\(\lambda =600 nm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1શરૂઆતમાં સમાંતર એવું નળાકાર કિરણજૂથ $\mu( I )=\mu_{0}+\mu_{2} I$ ધન વક્રીભવનાંકવાળા માધ્યમમાં પસાર થાય છે. અહી $\mu_{0}$ અને $\mu_{2}$ એ ધન અચળાંકો છે અને $I$ એ કિરણજૂથની તીવ્રતા છે. ત્રિજ્યામાં વધારા સાથે કિરણજૂથની તીવ્રતામાં ઘટાડો થાય છે.View Solution
આ કિરણજૂથ દ્વારા રચાતા તરંગઅગ્રનો શરૂઆતનો આકાર કેવો હશે?
- 2$10\, cm $ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી $25\, cm$ દૂર $3\, cm$ નો ચોરસ મૂકેલો છે. ચોરસનું કેન્દ્ર અરીસાની અક્ષ પર અને સમતલ અક્ષને લંબ છે. વાયરના પ્રતિબિંબ દ્વારા ઘેરાતું ક્ષેત્રફળ ........$cm^{2}$ છે.View Solution
- 3View Solutionજ્યારે પ્રકાશના કિરણપૂંજ ને સમતલ અરીસા પર આપાત કરવામાં આવે છે, ત્યારે તે વાસ્તવિક પ્રતિબિંબ રચે છે. તો આપાત કિરણપૂંજ કેવું હોવું જોઈએ ?
- 4View Solutionપ્રકાશનું કિરણ એક માધ્યમમાંથી બીજા માધ્યમમાં જાય ત્યારે,તેનો કયો ગુણધર્મ બદલાય છે?
- 5$t$ જાડાઈની અને $n$ વક્રીભવનાંકવાળી કાચની પ્લેટમાંથી પ્રકાશ પસાર થાય છે. જો શૂન્યાવકાશમાં પ્રકાશનો વેગ $c$ હોય, તો આ જાડાઈની કાચની પ્લેટમાંથી પ્રકાશને પસાર થવા માટે કેટલો સમય લાગશે?View Solution
- 6એક વસ્તુને અંતર્ગોળ અરિસાના વક્રતાકેન્દ્ર ${C}$ થી દૂર મૂકેલો છે. જો વસ્તુ અંતર ${C}$ થી ${d}_{1}$ અંતરે અને પ્રતિબિંબ ${C}$ થી ${d}_{2}$ અંતરે બને છે, તો અરિસાની વક્રતાત્રિજયા કેટલી હશે?View Solution
- 7એક બિંદુવત પ્રકાશનો સ્ત્રોત $\mu = 5/3$ વક્રીભવનાંકવાળા પાણીની સપાટીથી $4 \,\,cm$ નીચે મૂકેલો છે. પાણીમાંથી બહાર આવતાં સમગ્ર પ્રકાશને રોકવા માટે કેટલા લઘુત્તમ વ્યાસની તકતી ઉદ્દગમ પર મૂકવી જોઈએ........$m$View Solution
- 8બે $20\, mm$ કેન્દ્રલંબાઈ ધરાવતા ધન લેન્સમાંથી માઇક્રોસ્કોપ બનાવવામાં આવે છે જેમાં વસ્તુ વસ્તુકાંચથી $25\, mm$ અંતરે પડેલ છે. તો બંન્ને લેન્સને કેટલા દૂર($mm$ માં) ગોઠવવા જોઈએ કે જેથી અંતિમ પ્રતિબિંબ અનંત અંતરે મળે?View Solution
- 9$8m$ ઊંડાઇ ધરાવતી ટાંકીમાં પાણી ($\mu = 4/3$) ભરેલ છે.તો તળિયું કેટલી ઊંડાઇ પર દેખાય?View Solution
- 10એક તરવૈયો પાણીની અંદરથી બહારની બાજુ વર્તુળાકાર ક્ષેત્રમાં જોવે છે. પાણીનો વક્રીભવનાંક $\frac{4}{3}$ અને તરવૈયાની આંખ પાણીની સપાટીથી $15\, cm$ ઊંડાઈએ છે. તો તેને બહાર દેખાતા ક્ષેત્રના વર્તુળની ત્રિજ્યા કેટલી હશે?View Solution