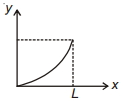
નીચે આપેલ ક્યા ગ્રાફ માંથી પોતાનાજ વજનના લીધે થતુ વિસ્તરણ $(y) \rightarrow$ સળીયાની લંબાઈનો સંપૂર્ણ સાચો ગ્રાફ દર્શાવે છે.
- A
- B
- C
- D
Medium
Download our app for free and get started
a
(a)
(a)
For elongation of rod under its own weight
We know \(\Delta x=\frac{\rho g x^2}{2 Y}\) \(\left\{\begin{array}{l}\text { Where, } \\ \Delta x=\text { Elongation } \\ \rho=\text { Density of rod } \\ Y=\text { Young's modulus } \\ L=\text { Length } \\ g=\text { Acceleration due to gravity } \\ x=\text { Distance of point from lower end }\end{array}\right.\)
We can clearly see that elongation \(\propto\left(x^2\right)\)
So graph of \(\Delta x\) vs \(x\) should be a upward parabola.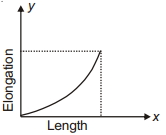
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો વાયુનું કદમાં ચાર ગણો વધાર્પ અને તાપમાન $27 ^\circ C$ થી $127 ^\circ C$ વધે તો સ્થિતિસ્થાપકતા કેટલી થાય ?View Solution
- 2તારનો પૃથ્વીની સપાટી ઉપર લંબાઈમાં વધારો $10^{-4} \,m$ છે. આ જ પરિમાણ ધરાવતા આ જ તારનો બીજા ગ્રહ પર લંબાઈનો વધારો $6 \times 10^{-5} \,m$ થાય છે. તે ગ્રહ પર ગુરૂત્વીય પ્રવેગ ............ $ms ^{-2}$ હશે, પૃથ્વીની સપાટી ઉપર ગુરૂત્વપ્રવેગનું મૂલ્ય $10 \,ms ^{-2}$ છે.View Solution
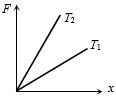
- 3નીચેના ગ્રાફમાં એક પાતળા તાર માટે બે તાપમાન $T_1$ અને $T_2$ માટે પ્રતિબળ વિરુદ્ધ લંબાઈમાં થતો ફેરફાર દર્શાવેલ છે તો તે શું દર્શાવે છે $?$View Solution
- 4$4\, mm$ વ્યાસ અને $9 \times {10^{10}}\,N/{m^2}$ યંગ મોડયુલસ ધરાવતા તારની લંબાઇ $0.1\%$ વધારવા માટે કેટલું બળ લગાવવું પડે?View Solution
- 5$20 \times {10^8}N/{m^2}$ નું પ્રતિબળ લગાવતા સંપૂર્ણ સ્થિતિસ્થાપક તારની લંબાઈ બમણી થઈજતી હોય તો યંગ મોડ્યુલસનું મૂલ્ય કેટલું હશે?View Solution
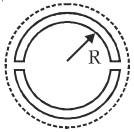
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે $R$ ત્રિજ્યાનું લાકડાનું પૈડું, બે અર્ધવર્તુળ ભાગોમાંથી બનેલું છે. આ બંને ભાગને ધાતુની એક રીંગ વડે સાથે જોડેલ છે. રીંગના આડછેડનું ક્ષેત્રફળ $S$ અને લંબાઈ $L$ છે. $L$ એ $2 \pi R$ કરતાં નાનું છે. તેથી રીંગને પૈડા પર ફીટ કરવા માટે ગરમ કરવા $T$ જेટલું તાપમાન વધારવામાં આવે છે. જેથી તે પૈડા પર માત્ર ગોઠવાઈ જાય છે. જ્યારે તેને ઓરડાના તાપમાન સુધી ઠંડુ પાડવામાં આવે છે ત્યારે તે અર્ધવર્તુળ પैડાના ભાગોને એકબીજા સાથે દબાણથી જોડી દે છે. જો ધાતુનો રેખીય પ્રસરણાંક $\alpha$ અને યંગ મોડ્યુલ્સ $Y$ હોય તો પैડાના એક ભાગ દ્વારા બીજા ભાગ પર કેટલું બળ લાગતું હશે?View Solution
- 7$10\, m$ લાંબા રબરના તારને શિરોલંબ લટકાવેલો હોય તો પોતાના વજનને લીધે તેની લંબાઈ કેટલી વધે $?($રબરની ઘનતા $1500\, kg/m^3$,$ Y = 5×10^8 N/m^2$, $g = 10 m/s^2$)View Solution
- 8નીચે આપેલ ક્યા ગ્રાફ માંથી પોતાનાજ વજનના લીધે થતુ વિસ્તરણ $(y) \rightarrow$ સળીયાની લંબાઈનો સંપૂર્ણ સાચો ગ્રાફ દર્શાવે છે.View Solution
- 9$1 \mathrm{~m}$ લંબાઈના એક સ્ટીલના તાર માટે જો સ્થિતિસ્થાપકતા સીમા અને યંગ મોડ્યુલ્સ અનુક્રમે $8 \times 10^8 \mathrm{~N} \mathrm{~m}^{-2}$ અને $2 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$ હોય તો તારમાં મહત્તમ ખેંચાણા (લંબાઈમાં વધારો). . . . . . . . .થશે.View Solution
- 10$1\,m{m^2}$ આડછેદ ધરાવતા તારની લંબાઇમાં $1\%$ વધારો કરવા માટે એકમ કદ દીઠ કરવું પડતું કાર્ય કેટલું થાય? $[Y = 9 \times {10^{11}}\,N/{m^2}]$View Solution