નીચે આપેલા પ્રગામી તરંગના સમીકરણમાંથી કયા તરંગોનો ઉપયોગ સ્થિત તરંગ ઉત્પન્ન કરવા માટે થાય?
$ {z_1} = A\sin (kx - \omega \,t) $ , $ {z_2} = A\sin (kx + \omega \,t) $ , $ {z_3} = A\sin (ky - \omega \,t) $ .
Medium
Download our app for free and get started
a
(a) Waves \({Z_1} = A\sin (kx - \omega t)\) is travelling towards positive \(x-\)direction.
(a) Waves \({Z_1} = A\sin (kx - \omega t)\) is travelling towards positive \(x-\)direction.
Wave \({Z_2} = A\sin (kx + \omega t)\), is travelling towards negative \(x-\)direction.
Wave \({Z_3} = A\sin (ky - \omega t)\) is travelling towards positive \(y\) direction.
Since waves \(Z_1\) and \(Z_2\) are travelling along the same line so they will produce stationary wave.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પિંપુડીઓ કે જેમની મૂળભૂત આવૃત્તિઓ $n_1 $ અને $ n_2 $ છે.તેમને શ્રેણીમાં જોડેલ છે. આ રીતે મેળવેલ નવી પિંપુડીની મૂળભૂત આવૃત્તિ થશે.View Solution
- 2નીચેની આકૃતિમાં એક સમાન પરિસ્થિતિ હેઠળ ચાર હવાસ્તંભનું દોલન દર્શાવેલ છે તેની આવૃતિનો ગુણોત્તર $n_p: n_q: n_r: n_s$ કેટલો હશે.View Solution
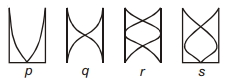
- 3ઉદ્ગમથી $1m$ અંતરે ધ્વનિની તીવ્રતા $40dB$ છે,માણસની થ્રેશોલ્ડ તીવ્રતા $20dB$ હોય,તો કેટલા ... $m$ મહત્તમ અંતર સુધી તે અવાજ સાંભળી શકે?View Solution
- 4બે તરંગો $ {y_1} = 10\sin \left( {3\pi t + \frac{\pi }{3}} \right) $ અને $ {y_2} = 5(\sin 3\pi t + \sqrt 3 \cos 3\pi t) $ ના કંપવિસ્તારનો ગુણોત્તર કેટલો થાય?View Solution
- 5$90 \mathrm{~cm}$ લંબાઈના અનુનાદ્દીય તાર ધરાવતા એક સોનોમીટર ને અમુક તણાવવાળી સ્થિતિમાં રાખવામાં આવે છે ત્યારે તેની મૂળભૂત આવૃત્તિ $400 \mathrm{~Hz}$ મળે છે. આ જ તણાવ માટે $600 \mathrm{~Hz}$ ની મૂળભૂત આવૃત્તિ મળે તે માટેની અનુનાદીય તાર ની લંબાઈ. . . . . . . $\mathrm{cm}$ હશે.View Solution
- 6$1.5$ $m$ લંબાઇ ધરાવતો એક સોનોમીટર વાયર સ્ટીલનો બનેલો છે.તેમાં લગાવેલ તાણને કારણે તેમાં $1 \%$ ની સ્થિતિસ્થાપકતા વિકૃતિ ઉત્પન્ન થાય છે.જો સ્ટીલની ઘનતા અને સ્થિતિસ્થાપકતા અનુક્રમે $7.7 \times 10^3 $ $kg/m^3$ અને $2.2 \times 10^{11}$ $N/m^2$ હોય,તો સ્ટીલની મૂળભૂત આવૃત્તિ .... $Hz$ શોધો.View Solution
- 7એક અવલોકનકાર $18\,km/h$ ની ઝડપ સાથે ટેકરી તરફ સાયકલ પ૨ ગતિ કરે છે. તે તેની પાછળ રહેલ ઉદગમમાંથી સીધો અવાજ સાંભળે છે ઉપરાંત ટેકરીથી પરાવર્તિત અવાજ પણ સાંભળે છે. ઉદગમ દ્વારા ઉત્પન્ન મૂળ આવૃત્તિ $640\,Hz$ હોય અને હવામાં ધ્વનિનો વેગ $320\,m / s$ હોય તો અવલોકનકાર દ્વારા આ બે અવાજે (ધ્વનિનો) વચ્ચે સંભળાતા સ્પંદની આવૃત્તિ $..........Hz$ હશે.View Solution
- 8View Solutionડોપ્લર અસર કયાં તરંગોમાં થાય?
- 9સ્ત્રોતબિંદુથી $4$ મીટર દૂરના બિંદુુએ અવાજની પ્રબળતા $10 \,dB$ છે, તો સ્રોતથી $2$ મીટર દુરના બિંદુએે પ્રબળતા ........ $dB$ હશે.View Solution
- 10બંધ પાઇપની મૂળભૂત આવૃત્તિ $ f. $ હોય,તો તેવી ખુલ્લી પાઇપની મૂળભૂત આવૃત્તિ .... $f$ કેટલી થાય?View Solution