નીચે આપેલાને સ્થાયિતાના વધતા ક્રમમાં ગોઠવો
$1.\,\,(CH_3)_2 - \mathop C\limits^ + - CH_2 - CH_3$
$2.\,\,(CH_3)_3 - \mathop C\limits^ + $
$3.\,\,(CH_3)_2 - |\mathop C\limits^ + H|$
$4.\,\,CH_3 - \mathop C\limits^ + H_2$
$5.\,\,\mathop C\limits^ + H_3$
NEET 2013, Medium
Download our app for free and get started
a
stability of carbocations follows following trendmethyl
stability of carbocations follows following trendmethyl
\(<1^{\circ}<2^{\circ}<3^{\circ}\)
Given carbocations \((\mathrm{CH} _3) _3 \mathrm{C} \cdot \Rightarrow 3^{\circ}\) carbocation
\((\mathrm{CH} _3) _2 \mathrm{CH} \cdot=>2^{\circ}\) carbocation
\(\mathrm{CH} _3 \mathrm{CH} _2 \cdot \Rightarrow 1^{\circ}\) carbocation
Therefore, increasing order of stability of carbocations \(\mathrm{CH} _3 \mathrm{CH}_ 2 \cdot\left(1^{\circ}\right)<(\mathrm{CH}_ 3) _2 \mathrm{CH} \cdot\left(2^{\circ}\right)<(\mathrm{CH}_3)_ 3 \mathrm{C} \cdot\left(3^{\circ}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
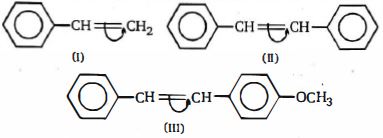
- 1સૂચવેલા મુજબ, $C = C$ બંધ વિશે પરિભ્રમણ અવરોધના નીચેનામાંથી કયા ક્રમ યોગ્ય છે?View Solution
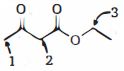
- 2ત્રણ જુદા જુદા કાર્બન(lલગાડેલા $1, 2$ & $3$). પરમાણુ સાથે જોડાયેલા હાઇડ્રોજન અણુઓને ધ્યાનમાં લોમોટાભાગના એસિડિકથી ઓછામાં ઓછા એસિડિક સુધી ક્રમમાં જોડાયેલ હાઇડ્રોજન અણુઓને ક્રમ આપોView Solution
- 3કયો દ્વિતીયક મૂલક છે ?View Solution
$(1)$ $C{H_3} - \mathop {CH}\limits^| - {C_2}{H_5}$
$(2)$ $C{H_2} = \,\mathop C\limits^| \, - \,\,C{H_3}$
$(3)$ $ CH_2 = CH -$
$(4)$ $(CH_3)_2 CH -$
- 4કયો મહત્તમ $pK_a$ ધરાવે છે ?View Solution
- 5View Solutionનીચેનામાંથી કયો કેન્દ્રાનુરાગી દ્વારા સૌથી સરળ રીતે હુમલો કરી શકે છે ?
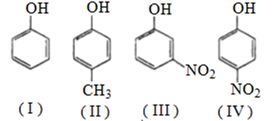
- 6View Solutionનીચેના પદાર્થો માટે એસિડિકતાનો ક્રમ કયો છે ?
- 7View Solutionનીચે પૈકી કયું સૌથી વધારે સ્થિર છે?
- 8નીચેની પ્રક્રિયા $(CH_3)_3C - Br + H_2O \rightarrow (CH_3)_3C-OH + HBr$ કઈ પ્રક્રિયાનું ઉદાહરણ છે.View Solution
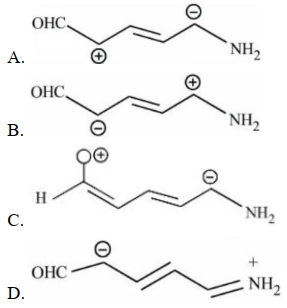
- 9View Solutionસસ્પંદ બંધારણોની સ્થિરતાનો ચઢતો ક્રમ શોધો.
- 10View Solutionઅયુગ્મિત ઇલેકટ્રૉનની હાજરીને લીધે મુકત મૂલકો ....... બને છે.