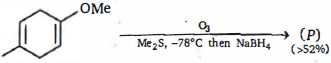નીચે આપેલી પ્રક્રિયામાં $C{H_3} - C{H_2} - C{H_2} - C{H_3} \xrightarrow[475\, K]{H_2SO_4}$
AIIMS 1983, Medium
Download our app for free and get started
a
(a) $C{H_3} - C{H_2} - C{H_2} - C{H_3} \xrightarrow[475\, K]{H_2SO_4}$ $\mathop {C{H_3} - CH = CH - C{H_3}}\limits_{{\rm{More \,symmetrical\,}}\,({\rm{major}}\,{\rm{\,product)}}} $
(a) $C{H_3} - C{H_2} - C{H_2} - C{H_3} \xrightarrow[475\, K]{H_2SO_4}$ $\mathop {C{H_3} - CH = CH - C{H_3}}\limits_{{\rm{More \,symmetrical\,}}\,({\rm{major}}\,{\rm{\,product)}}} $
$C{H_3} - C{H_2} - C{H_2} - C{H_3}\xrightarrow[{475\,K}]{{{H_2}S{O_4}}} $$\mathop {C{H_2} = CH - C{H_2} - C{H_3}}\limits_{{\text{Less}}{\mkern 1mu} {\text{symmetrical}}{\mkern 1mu} {\text{or}}{\mkern 1mu} {\text{unsymmetrical}}{\mkern 1mu} ({\text{minor}}{\mkern 1mu} {\text{product}})} $
It is based on Saytzeff's rule. According to this more symmetrical or more alkylated alkene predominates.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$H_2\, (Pd/C)$ સાથે આપેલ પ્રકીયકો ના ઉત્પ્રેરક હાઇડ્રોજનરેશન પર ઉષ્ણતામાનનો ઘટાડો થયો એનો ક્રમ ક્યો છે ?View Solution
- 2View Solutionપ્રોપીનમાંથી પ્રોપેન કઈ પદ્ધતિ દ્વારા મેળવવામાં આવે છે?
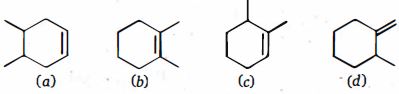
- 3View Solutionઆપેલી પ્રકિયા માં મુખ્ય નીપજ કઈ હશે ?
- 4View Solutionસોડિયમ એસિટેટ અને સોડિયમ પ્રોપિયોનેટ ધરાવતા જલીય દ્રાવણના વિધુતવિભાજનથી .......... મળે છે.
- 5View Solutionબેન્ઝિનમાં પ્રત્યેક કાર્બન-કાર્બન બંધનો બંધ-ક્રમાંક શું છે?
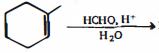
- 6આ પ્રકિયા ની $(A)$ નીપજ શું હશે ?View Solution
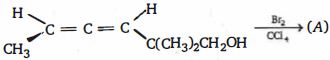
- 7$(C_5H_9Cl)$ નો પ્રકાશિય સમઘટક $(A)$ તેની પ્રકિયા હાઈડ્રોજન ના એક મોલ આપે છે. નિષ્ક્રિય પ્રકાશક્રિયાશીલ સંયોજન $(B)$ સંયોજન $(A)$ શું હશે ?View Solution
- 8સૂર્યપ્રકાશની હાજરીમાં $2-$મિથાઇલ બ્યુટેનની બ્રોમીન સાથેની પ્રક્રિયાથી મુખ્યત્વે ...... મળે છેView Solution
- 9નીચેનામાંથી પ્રકીયક $(A)$ શું હોય શકે ?View Solution
- 10આપેલ પ્રક્રિયામાં, ફક્ત એક જ આલ્કીન ઇલેક્ટ્રોઅનુરાગી ઓઝોન દ્વારા પ્રેફરન્શિયલ ઓક્સિડેશનમાંથી પસાર થાય છે. આપેલ પ્રક્રિયાની નીપજ $(P)$ શોધો.View Solution
