Download our appand get started for free
Similar Questions
- 1$5\, km$ પહોળાઈ અને $5\, km$ લંબાઈ ધરાવતો એક વિશાળ જળવાદળ છે. તેનું તળિયું (પાયો અહી દર્શાવ્યા પ્રમાણે પૃથ્વીની સપાટીથી $1\, km$ ઉપર છે. ડાઈ ઈલેકટ્રીક તરીકે હવાના માધ્યમ સાથે પૃથ્વીની સપાટી અને વાદળને સમાંતર પ્લેટ કેપેસિટર હોય તેમ ધારો તો વાદળ અને પૃથ્વી સપાટી સંયોજનનું કેપેસિટન્સ........$\mu F$ માં શોધો.View Solution

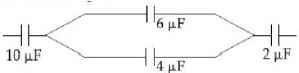
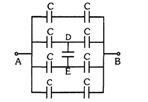
- 2આપેલ આકૃતિમાં પરિણામી કેપેસિટન્સ $C_{AB}$ =......$C$View Solution
- 3$0.2\,F$ કેપેસિટરને $600\,V$ ની બેટરી સાથે જોડેલ છે.હવે બેટરી દૂર કરીને $1\,F$ ના કેપેસિટર સાથે જોડતાં, નવો વોલ્ટેજ કેટલા........$volts$ થાય?View Solution
- 4$100\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $E$ છે. $60\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $\sqrt{\frac{x}{5}} E$ હોય તો તો $x$નું મૂલ્ય કેટલું હશે?View Solution
- 5નીચે બે વિધાનો આપેલાં છે. એકને કથન $A$ અને બીજાને કારણા $R$ વડે દર્શાવેલ છે.View Solution
કथન $A: 4 \times 10^{-6} \mathrm{C}$ $m$ના મૂલ્યની દ્રી-ધ્રુવી ચાકમાત્રા $\vec{P}$. ધરાવતી દ્રી-ધ્રુવીના કેન્દ્રથી $2 \mathrm{~m}$ અંતરે $(r)$ રહેલ કોઈ અક્ષીય બિંદુ આગળ સ્થિતિમાન $(\mathrm{V}) \pm 9 \times 10^3 \mathrm{~V}$ છે.
$\left[\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \text { SI એકમ }\right]$
કારણ $R: V= \pm \frac{2 P}{4 \pi \epsilon_0 r^2}$, જ્યાં $r$ એ કોઈ અક્ષીય બિંદુનું
ત્રિજ્યાવર્તી દિશામાં અંતર છે કે જે દ્વિ-ધ્રુવીનાં કેન્દ્રથી $2 \mathrm{~m}$ અંતરે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિક્લ્પોમાંથી સાચો ઉત્તર ૫સંદ કરો.
- 6$6\ cm$ ત્રિજયા ઘરાવતા ગોળીય કવચને સમકેન્દ્રિત રહે તેમ $4\ cm$ ત્રિજયા ઘરાવતો ગોળો મુકેલ છે. બહારની ગોળીય કવચને ગ્રાઉન્ડ કરેલી છે.જો અંદરના ગોળાનો વોલ્ટેજ $3\ e.s.u$ હોય તો તેમાં વિદ્યુતભાર કેટલા .......$ e.s.u.$ થાય?View Solution
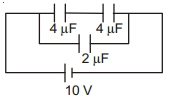
- 7જો આપેલી આકૃતિમાં દર્શાવ્યા મુજબનાં કેપેસીટરોનો પ્રારંભીક ચાર્જ શૂન્ય હોય તો દર્શાવેલ બેટલી દ્વારા થતું કાર્ય ......... $mJ$ હશે.View Solution
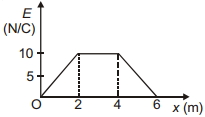
- 8આકૃતિમાં દર્શાવ્યા મુજબનો આલેખ વિદ્યુતક્ષેત્રની તીવ્રતા $E$ ને અંતરના $x$ નાં સાપેક્ષે દર્શાવેલ છે. ઉગમબિંદુ $O$ થી $x=2\,m$ અને $x=6\,m$ પરનાં બિંદુઓ વચ્ચે સ્થિતિમાનનો તફવવત $\dots\dots V$ હશે.View Solution
- 9વિજભારના વિતરણ માટે વિદ્યુતસ્થિતિમાન($volt$ માં)View Solution
$V(z)\, = \,30 - 5{z^2}for\,\left| z \right| \le 1\,m$
$V(z)\, = \,35 - 10\,\left| z \right|for\,\left| z \right| \ge 1\,m$
મુજબ આપવામાં આવે છે જ્યાં $V(z)$ એ $x$ અને $y$ પર આધારિત નથી. અમુક સપાટીમાં પથરાયેલ એકમ કદદીઠ અચળ વિજભાર $\rho _0$($\varepsilon _0$ ના એકમમાં) માટે વિદ્યુતસ્થિતિમાન આપેલ છે. તો નીચેનામાંથી કયું વિધાન સાચું પડશે?
- 10$27$ એક સમાન બુંદોને દરેકને $22 \,V$ થી વિદ્યુત ભારીત કરવામાં આવે છે. તેઓ સંયોજાઈને એક મોટું બુંદ બનાવે છે. મોટાં બુંદનું સ્થિતિમાન.......$V$ થશે.View Solution