$(A)\;y= sin\omega t-cos\omega t$
$(B)\;y=sin^3\omega t$
$(C)\;y=5cos\left( {\frac{{3\pi }}{4} - 3\omega t} \right)$
$(D)\;y=1+\omega t+{\omega ^2}{t^2}$
\(y=\sin \omega t-\cos \omega t\)
\(=\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin \omega t-\frac{1}{\sqrt{2}} \cos \omega t\right]=\sqrt{2} \sin \left(\omega t-\frac{\pi}{4}\right)\)
It represents a \(SHM\) with time period, \(T=\frac{2 \pi}{\omega}\)
\(y=\sin ^{3} \omega t=\frac{1}{4}[3 \sin \omega t-\sin 3 \omega t]\)
It represents a periodic motion with time period
\(T=\frac{2 \pi}{\omega}\) but not \(SHM\)
\(y =5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right) \)
\(=5 \cos \left(3 \omega t-\frac{3 \pi}{4}\right) \quad[\because \quad \cos (-\theta)=\cos \theta]\)
It represents a \(SHM\) with time period, \(T=\frac{2 \pi}{3 \omega}\)
\(y=1+\omega t+\omega^{2} t^{2}\)
It represents a non-periodic motion. Also it is not physically acceptable as \(y \rightarrow \infty\) as \(t \rightarrow \infty\)
Download our appand get started for free
Similar Questions
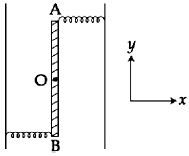
- 1$l$ લંબાઈના અને $m$ દ્રવ્યમાનના એક સમક્ષિતિજ સળીયા $AB$ ના બે છેડાઓ પર $k$ સ્પ્રિંગ અચળાંક ધરાવતી બે હલકી સમાન સ્પ્રિંગો સમક્ષિતિજ જોડેલ છે. આ સળીયો તેના કેન્દ્ર $O$ થી જડેલ છે. અને તે સમક્ષિતિજ સમતલમાં મુક્ત ભ્રમણ કરી શકે છે. આકૃતિમાં બતાવ્યા પ્રમાણે બે સ્પ્રિંગોના બીજા છેડાઓ જડ આધાર સાથે જોડેલ છે. આ સળિયાને હળવેકથી ધક્કો મારી કોઈ નાના ખુણે ફેરવીને છોડી દેવામાં આવે તો પરિણામી દોલનની આવૃત્તિ કેટલી થાય?View Solution
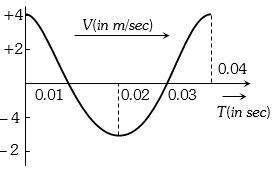
- 2સરળ આવર્તગતિ માટે વેગ વિરુઘ્ઘ સમયનો આલેખ આપેલ છે.તો આવૃત્તિ કેટલી ..... $Hz$ થાય?View Solution
- 3View Solutionઅવમંદિત સરળ આવર્તગતિમાં વેગ અને સ્થાનાંતર નો આલેખ કેવો મળે?
- 4View Solutionસરળ આવર્ત ગતિ કરતાં એક કણના સ્થાનાંતર અને પ્રવેગ વચ્ચેનો કળા તફાવત .......... છે
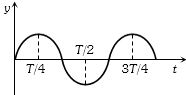
- 5View Solutionસરળ આવર્તગતિ માટે સ્થાનાંતર વિરુઘ્ઘ સમયનો આલેખ આપેલ છે તો નીચે પૈકી શું સાચું થાય?
- 6$x = 0.01\sin 100\pi (t + 0.05)$ હોય,તો સરળ આવર્તગતિનો આવર્તકાળ કેટલો ... $\sec$ થાય?View Solution
- 7k બળ અચળાંક ધરાવતી સ્પ્રિગ સાથે દળ $m$ જોડવામાં આવેલ છે અને તે મુજબ સપાટી જોડેલ છે.અને તે આકૃતિ મુજબ સપાટી જોડેલ બીજી સ્પ્રિંગને અડે છે. નાના દોલનોનો આવર્તકાળ કેટલો થાય?View Solution
- 8પૃથ્વી પર એક સેકન્ડનો આવર્તકાળ ધરાવતું લોલક એવા ગ્રહ પર લઈ જવામાં આવે છે કે જ્યાં ગુરૂત્વાર્ષણળ બળ $4$ ગણું છે. આ ગ્રહ પર એક સેકન્ડ આવર્તકાળ દર્શાવતા લોલકની લંબાઈ ............ ગણી કરવી જોઈએ ?View Solution
- 9સરળ આવર્તગતિ કરતાં એક કણની યાંત્રિક ઊર્જા $90 \,J$ અને કંપવિસ્તાર $6 \,cm$ છે. જો તેની ઊર્જા ઘટીને $40 \,J$ જેટલી થાય તો કંપવિસ્તાર કેટલો થશે તે જાણાવો.View Solution
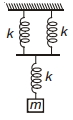
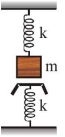
- 10એક સરખા સ્પ્રિંગ અચળાંક $k$ ધરાવતી ત્રણ સ્પ્રિંગ સાથે $m$ જેટલું દળ આકૃતિ મુજબ લટકાવેલ છે. જો દળને થોડુંક નીચે તરફ ખેંચીને છોડી દેવામાં આવે તો થતા દોલનોનો આવર્તકાળ કેટલો હશે ?View Solution