નીચેના માંથી ક્યાં સંબંધો સાચાં છે?
$(A)$ $\Delta U = q + p \Delta V$
$(B)$ $\Delta G =\Delta H - T \Delta S$
$(C)$ $\Delta S =\frac{ q _{ rev }}{ T }$
$(D)$ $\Delta H =\Delta U -\Delta nRT$
નીચે આપેલા વિકલ્પોમાંથી યોગ્ય ઉત્તર પસંદ કરો.
JEE MAIN 2023, Medium
Download our app for free and get started
b
Only $(B)$ and $(C)$ are correct.
Only $(B)$ and $(C)$ are correct.
$(B)$ $G = H - TS$
At constant $T$
$\Delta G =\Delta H - T \Delta S$
(A) First law is given by
$\Delta U = Q + W$
If we apply constant $P$ and reversible work
$\Delta U = Q - P \Delta V$
(C)By definition of entropy change
$dS =\frac{ dq _{ rer }}{ T }$
At constant $T$
$\Delta S=\frac{q_{\text {rev }}}{T}$
(D) $H = U + PV$
For ideal gas
$H = U + nRT$
At constant $T$
$\Delta H =\Delta U +\Delta nRT$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસમોષ્મી પ્રક્રિયા માટે નીચેનામાંથી કયો સંબંધ સાચો છે ?
- 2એસીટીલીનની નિર્માણ ઉષ્મા .....$KJ$ માં શોધો.View Solution
$2 \mathrm{C}_{(\mathrm{s})}+2 \mathrm{O}_2(\mathrm{~g}) 2 \mathrm{CO}_2(\mathrm{~g}), \Delta \mathrm{H}=-787 \mathrm{KJ} ; \mathrm{H}_2(\mathrm{~g})+$$\mathrm{H}_2 \mathrm{O}, \Delta \mathrm{H}=-286 \mathrm{KJ}$
$\frac{1}{2} \mathrm{O}_2 \mathrm{C}_2 \mathrm{H}_2(g)+\frac{5}{2} \mathrm{O}_2(g) \rightarrow 2 \mathrm{CO}_2(g)+\mathrm{H}_2 \mathrm{O}(I), \Delta H=-1310KJ$
- 3${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( g \right)}};\Delta {H_1}$ અનેView Solution
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}};\Delta {H_2}$ હોય, તો
- 4$350\,K$ પર આદર્શ વાયુ અને $4\,atm$ થર્મલ વાહક દિવાલોના $2.0\,L$ પાત્રમાં હોય છે, જે પર્યાવરણના સંપર્કમાં હોય છે.તે $4\,atm$ ના અચળ દબાણ વિરુદ્ધ સમતાપી પ્રતિવર્તી $........\,J\,K ^{-1}$ છે.(નજીકનો પૂર્ણાક) આપેલ : $R =8.314\,J\,K ^{-1}\,mol ^{-1}$.View Solution
- 5$2Zn + O_2$ $\rightarrow$ $2ZnO, \Delta G^o = -616 \,J ; 2Zn + S_2$ $\rightarrow$ $2ZnS$, $\Delta G^o = -293\, J; S_2 + 2O_2$ $\rightarrow$ $2SO_2$, $\Delta G^o = -408 \,J$View Solution
તો $2ZnS + 3O_2$ $\rightarrow$ $2ZnO + 2SO_3$ પ્રક્રિયા માટે $\Delta\, G^o$ નું મૂલ્ય .......$J$
- 6View Solutionબોમ્બ કેલરીમીટરમાં પ્રક્રિયા માટે માપવામાં આવતી ઉષ્માનું પ્રમાણ છે?
- 7$C$, $S$ અને $CS_2$ ની દહન-ઉષ્મા અનુક્રમે $x, y$ અને $z\,kJ\,mol^{-1}$ હોય તો $CS_2$ ની સર્જન-ઉષ્મા કેટલી થશે ?View Solution
- 8$10\, atm$. દબાણે અને $300\, K$ તાપમાને રહેલા વાયુનુ $5\, atm$.દબાણે અને $290\, K$ તાપમાને સમોષ્મી પ્રતિવર્તી વિસ્તરણ થાય છે. તો વાયુની મોલર ઉષ્માક્ષમતા .....$cal\,mo{l^{ - 1}}$ થશે.View Solution
- 9$3$ -મીથાઈલબ્યુટિન અને $2$ પેન્ટીન માંટે હાઇડ્રોજનની ઉષ્મા અનુક્રમે $-30\, kcal/mol$ and $-28\,kcal/mol$ છે. $2$ -મિથાઈલબુટેને અને પેન્ટાઇનના દહનની ઉષ્મા છે - અનુક્રમે $784 \,kcal / mol$ અને $-782 \,kcal/mol$ બધા મૂલ્યો પ્રમાણભૂત શરતો હેઠળ આપવામાં આવે છે. તે ધ્યાનમાં લેતા કે બંને આલકેન્સના દહન સમાન નિપજો આપે છે, સમાન પરિસ્થિતિઓમાં નીચેની પ્રક્રિયા માટે $\Delta H$ (in $kcal/mol$) શું છે?View Solution
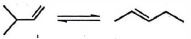
- 10View Solutionઉષ્માશોષક પ્રક્રિયા કઈ છે?