નીચેના પૈકી કયું કાર્બોકેટાયન વધુ સ્થાયી છે ?
Easy
Download our app for free and get started
b
\({\left( {C{H_3}} \right)_3}C.\mathop C\limits^ + {H_2}\) is a tertiary carbocation. A tertiary carbocation is the most stable carbocation due to the electron releasing effect of three methyl groups. An increased \(+I\) effect by three methyl groups stabilizes the positive charge on the carbocation.
\({\left( {C{H_3}} \right)_3}C.\mathop C\limits^ + {H_2}\) is a tertiary carbocation. A tertiary carbocation is the most stable carbocation due to the electron releasing effect of three methyl groups. An increased \(+I\) effect by three methyl groups stabilizes the positive charge on the carbocation.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેના આલ્કેન્સ સમ વિભાજન દ્વારા મુક્ત મુલક બનાવે છે.View Solution
$CH_3 - CH_3, CH_3 - CH_2 $$- CH_3, (CH_3)_2CH - CH_3,$
$ CH_3 - CH_2 - CH(CH_3)_2.$
આ મૂલકોનો સ્થાયિતાનો વધતો ક્રમ કયો છે?
- 2View Solutionએસિડિક પ્રબળતા ના વધતા ક્રમમાં નીચેના ને ગોઠવો
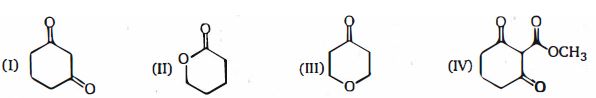
- 3View Solutionઆપેલા પ્રમાણભૂત બંધારણણો સાચો સ્થાયિતા ક્રમ કયો છે ?
- 4નિક્ટતમ પરમાણુ પર હાજર અબંધકારક ઈલેક્ટ્રોન યુગ્મ અને $\pi$ બંધ વચ્ચેની પારસ્પરિક ક્રિયા માટે જવાબદાર_____View Solution
- 5View Solutionકયો સમૂહ મહત્તમ અતિસંયુગ્મન અસર ધરાવે છે ?
- 6વિસ્થાપિત એનિલીન ($I$ થી $IV$) ના બેઝિક ગુણધર્મનો સાચો ક્રમ કયો છે ?View Solution
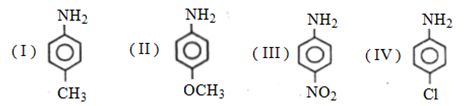
- 7આપેલ કાર્બોકેટાયન માટે સ્થિરતાનો સાચો કમ કયો છે ?$\mathop {\mathop C\limits^ \oplus {H_3}}\limits_{(i)} \,\,\,\,\,\,\,\,\,C{H_3}\mathop {\mathop C\limits^ \oplus {H_2}}\limits_{(ii)} \,\,\,\,\,\,\,\,\mathop {\mathop C\limits^ \oplus {H_2}}\limits_{(iii)} OC{H_3}\,$View Solution
- 8View Solutionનીચેના મુક્તમૂલકોની સ્થાયીતાનો સાચો વધતો ક્રમ .....
- 9કાર્બેનાયન્સની સ્થાયિતાનો ક્રમ શું છે?View Solution
$(i)\,\,RC \equiv \mathop C\limits^ \ominus $
$(ii)\,\,[IMAGE]$
$(iii)\,\,{R_2}C = \mathop C\limits^ \ominus H$
$(iv)\,\,{R_3}C - \mathop C\limits^ \ominus {H_2}$
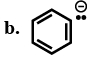
- 10View Solutionનીચેનામાંથી કયો પ્રબળ બેઈઝ છે ?