નીચેનામાંથી કયા સંયોજન માં સંસ્પંદન સ્થાયી નથી?
Diffcult
Download our app for free and get started
c
$(c)$ Lone pair will not participate in resonance because of bredt's rule.
$(c)$ Lone pair will not participate in resonance because of bredt's rule.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેના પદાર્થો માટે એસિડિકતાનો ક્રમ કયો છે ?
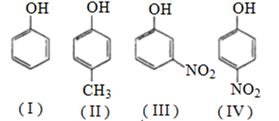
- 2નીચે આપેલ પૈકી, મેટા નિર્દેશક ક્રિયાશીલ સમૂહોની કુલ સંખ્યા __________છે. (પૂણાંક આધારિત)View Solution
$ -\mathrm{OCH}_3,-\mathrm{NO}_2,-\mathrm{CN},-\mathrm{CH}_3-\mathrm{NHCOCH}_3,$ $ -\mathrm{COR},-\mathrm{OH},-\mathrm{COOH},-\mathrm{Cl}$
- 3View Solutionનીચેનામાનથી કયું બેંઝિન નું વિસ્થાપન ઇલેક્ટ્રોનુરાગી વિસ્થાપન માં ઓર્થો-પેરા અને કેંદ્રાનુરાગી વિસ્થાપન માં ઓર્થો-પેરા માં છે
- 4View Solutionનીચેના કાર્બન કેટાયન ને ધ્યાનમાં લો. આ કાર્બોકેટાયનની સંલગ્ન સ્થિરતા કઈ છે?
- 5View Solutionનીચેનામાંથી કયા સ્થિર કાર્બોકેટાયન છે?
- 6View Solutionબેન્ઝીન ચક્રમાં નાઇટ્રો સમૂહની હાજરી
- 7View Solutionનીચે આપેલા ધનાયાનમાં સ્થિરતા (સૌથી વધુ સ્થિર થી ઓછામાં ઓછું સ્થિર) નો વધતો ક્રમ કયો છે?
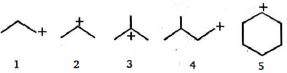
- 8નીચે આપેલા $H$ પરમાણુઓનો ચઢતો એસિડિકતતા ક્રમ શોધો.View Solution
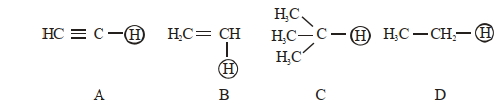
- 9આપેલ સંયોજનમાં $\alpha$ -હાઇડ્રોજનની કુલ સંખ્યા કેટલી છેView Solution
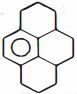
- 10કયો દ્વિતીયક મૂલક છે ?View Solution
$(1)$ $C{H_3} - \mathop {CH}\limits^| - {C_2}{H_5}$
$(2)$ $C{H_2} = \,\mathop C\limits^| \, - \,\,C{H_3}$
$(3)$ $ CH_2 = CH -$
$(4)$ $(CH_3)_2 CH -$