નીચેનામાંથી કયું સંયોજન ધન મેસોમેરિક અસર દર્શાવે છે ?
Medium
Download our app for free and get started
a
જે સમૂહ દ્વિબંધને \( e^- \) આપે છે. તેવી રચના \(+M\) અથવા \(+R\) અસર ધરાવે છે.
જે સમૂહ દ્વિબંધને \( e^- \) આપે છે. તેવી રચના \(+M\) અથવા \(+R\) અસર ધરાવે છે.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેના માટે ઈલેકટ્રોન અનુરાગી માટે ઘટતો પ્રક્રિયાશીલતા ક્રમ કયો છે ?View Solution
$(1)$ બેન્ઝીન $(2)$ ટોલ્યુઈન $(3)$ ક્લોરો બેન્ઝિન $(4)$ ફિનોલ
- 2આયનીકરણની સ્થિરતાનો ક્રમ કયો છે?View Solution
${\rm{(X)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,C{H_3}$
${\rm{(Y)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,O\,C{H_3}$
${\rm{(Z)}}{\rm{. }}C{H_3} - \,\,\,\mathop C\limits^ \oplus H\,\, - \,\,CO\,C{H_3}$
- 3View Solutionકાર્બનના સંકરણમાં ફેરફાર થાય તેની સાથે કાર્બન આયનની સ્થિરતાનો ચડતો ક્રમ કયો છે ?
- 4નીચેના પદાર્થમાં કાર્બન - કાર્બન એક બંધ લંબાઈનો ઘટતો ક્રમ કયો છે ?View Solution
$(I)$ $CH_2 = CH - C \equiv CH$
$(II)$ $CH \equiv C - C\equiv CH$
$(III)$ $CH_3 - CH = CH_2$
$(IV) $ $CH_2 = CH - C = CH_2$
- 5View Solutionનીચેના પૈકી ક્યુ સંયોજન અતિસંયુગ્મન દર્શાવે છે ?
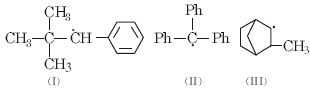
- 6View Solutionઉપરના સંયોજનો માટે ઈલેક્ટ્રોન અનુરાગી વિસ્થાપન ના ઉતરતા ક્રમ માટે સાચી ગોઠવણી શોધો.
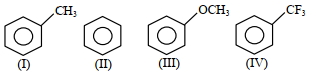
- 7એ.....View Solution
$\begin{matrix}
\overset{\Theta }{\mathop{\overset{\centerdot \,\centerdot }{\mathop{C}}\,}}\,{{H}_{2}}-C-C{{H}_{3}} \\
|| \\
O \\
\end{matrix}$ અને $\begin{matrix}
C{{H}_{2}}=C-C{{H}_{3}} \\
| \\
:\underset{\Theta }{\mathop{\underset{\centerdot \,\centerdot }{\mathop{O}}\,}}\,: \\
\end{matrix}$ - 8View Solutionસૌથી પ્રબળ એસિડ......... છે.
- 9આપેલા પરમાણુના નામાંકનમાં, $H$ અણું શામેલ છેView Solution
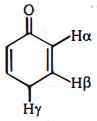
- 10સૂચવેલા મુજબ, $C = C$ બંધ વિશે પરિભ્રમણ અવરોધના નીચેનામાંથી કયા ક્રમ યોગ્ય છે?View Solution
