$(x)\begin{array}{*{20}{c}}
{O\,\,\,}\\
{||\,\,\,}\\
{C{H_3} - S - O - H}\\
{||\,\,\,\,}\\
{O\,\,\,\,}
\end{array}$
$\begin{array}{*{20}{c}}
{\,\,\,\,\,O}\\
{\,\,\,\,\,\,||}\\
{(y)\,\,\,C{H_3} - C - O - H}
\end{array}$
$(z)\,\, CH_3 -OH$
Stability of resonance hybrid \(\propto\) no. of equivalent \(R.S.\) So stability order is
\(\mathop {\begin{array}{*{20}{c}}
O \\
{||} \\
{Me - S - {O^\Theta }} \\
{||} \\
O
\end{array}}\limits_{3 - eq.\,R.S.} \) \(>\) \(\mathop {\begin{array}{*{20}{c}}
O \\
{||} \\
{Me - C - {O^\Theta }}
\end{array}}\limits_{2 - eq.\,R.S.} \) \(>\) \(Me - {O^\Theta }\)
So Acidic strength order is \(x>y>z\) so \(\mathrm{pK}_{\mathrm{a}}\) is \(z>y>x\)
Download our appand get started for free
Similar Questions
- 1View Solutionએસિડ્સની કેટલીક જોડીઓ નીચે આપેઌ છે. તે જોડી પસંદ કરો જેમાં પ્રથમ એસિડ વધુ પ્રબળ હોય
- 2View Solutionકેન્દ્ર અનુરાગીનો સાચો ક્રમ કયો છે.
- 3View Solutionકયો કાર્બોકેટાયન સૌથી સ્થાયી છે?
- 4View Solutionનીચેનામાંથી કયો પ્રબળ બેઈઝ છે ?
- 5કાર્બનની કઈ સ્પીસીઝ $e-$ નું ષષ્ટક ધરાવે છે અને ઈલેક્ટ્રોન અનુરાગી તરીકે વર્તે છે.View Solution
- 6કાર્બોકેટાયનને તેમની ઘટતી સ્થિરતાના ક્રમમાં ગોઠવો.View Solution
$(1) H_3C - C = C⊝\,(2) H - C = C⊝ \,(3) $ ${H_3}C\,\, - \,\,\mathop C\limits^\Theta {H_2}$
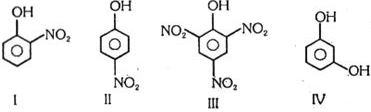
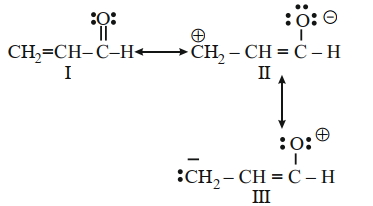
- 7View Solutionભાગ લેતાં બંધારણની સાપેક્ષ સ્થિરતાનો ક્રમ શોધો.
નીચે આપેલા વિકલપોમાંથી સાચો જવાબ પસંદ કરો.
- 8$H - C \equiv C\mathop {-} \limits^a C \equiv C\mathop {-} \limits^b C{H_3}$View Solution
$a$ અને $b$ ની બંધ લંબાઈની તુલના કરો
- 9View Solutionનીચેનામાંથી કયો ક્રમ ઘટતી એસિડિકતાનો સાચો ક્રમ આપે છે ?
- 10View Solutionનીચેના પદાર્થો માટે વધતા વિયોજન અચળાંકનો સાચો ક્રમ કયો છે ?