Depression in freezing point: \(\Delta T_{f}=i \times k_{f} \times m\)
where, \(\Delta T_{f}=\) depression in freezing point
\(\mathrm{i}=\mathrm{vant}\) hoff factor
\(k_{f}=\) freezing point constant
\(\mathrm{m}=\) molality
\(\mathrm{i}=\frac{\text { Total no on moles at equilibrium }}{\text { Init inl moles }}\)
\(\quad \quad H X \rightarrow H^{+}+X^{-}\)
\(\mathrm{l}: \quad 0.5\quad \quad 0 \quad \quad 0\)
\(\mathrm{C}: \mathrm{c}-\mathrm{c\alpha} \quad \mathrm{c\alpha} \quad \mathrm{c\alpha}\)
\(\alpha=\frac{20}{100}=0.2, c=0.5 \mathrm{M}\)
\(\mathrm{c}-\mathrm{c} \alpha=0.4 \mathrm{M}, \mathrm{c\alpha}=0.1 \mathrm{M}, \mathrm{c\alpha} = 0.1 \mathrm{M}\)
Total moles at equilibrium \(=0.4 \mathrm{M}+0.1 \mathrm{M}+0.1 \mathrm{M}=0.6 \mathrm{M}\)
\(i=\frac{0.6 M}{0.5 M}=1.2\)
Depression in freezing point: \(\Delta T_{f}=1.2 \times 1.86 \;K / kg\;mol\) \(\times 0.5 M=1.12\; K\)
Download our appand get started for free
Similar Questions
- 1View Solutionકયું ન્યૂનતમ ઠારણબિંદુ ધરાવે છે?
- 2$25^o C$ તાપમાને જુદા જુદા દ્રાવણો $0.500\, M\, C_2H_5OH\,(aq),$ $0.100\,M\,Mg_3(PO_4)_2\, (aq), $ $0.250\, M\,KBr\,(aq)$ અને $0.125\, M\,Na_3PO_4\,(aq)$ ને ધ્યાનમાં લો. બધા જ ક્ષારો પ્રબળ વિધુતવિભાજ્ય છે તેમ ધારતા આ દ્રાવણો માટે નીચેનામાંથી ક્યુ વિધાન સાચું છે ?View Solution
- 3$100 \mathrm{~g}$ પાણીમાં $10 \mathrm{~g}$ વિદ્યુતવિભાજ્ય $\mathrm{AB}_2\left(\mathrm{AB}_2 \rightarrow \mathrm{A}^{2+}+2 \mathrm{~B}^{-}\right)$ધરાવતું એક દ્રાવણ $100.52^{\circ} \mathrm{C}$ એ ઉકળે છે. વિદ્યુતવિભાજ્યનો આયનીકરણ અંશ $(\alpha)$. ......... $\times 10^{-1}$છે.View Solution
[ $\mathrm{AB}_2$ નું મોલર દળ $=200 \mathrm{~g} \mathrm{~mol}{ }^{-1}$, પાણીનું ઉત્કલનબિંદુ $=100^{\circ} \mathrm{C}, \mathrm{K}_{\mathrm{b}}$ (પાણીનો મોલલ ઉત્કલનબિંદુ ઉન્નયન અચળાંક $\left.=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)$ ]
- 4બે દ્રાવકો $X$ અને $Y$ માં એક વિધુતઅવિભાજ્ય, અબાષ્પશીલ દ્રાવ્ય ઓગાળીને બે અલગ અલગ $5$ મોલલ દ્રાવણો તૈયાર કરવામાં આવ્યા છે. દ્રાવકના આણ્વિય દળ અનુક્રમે $M_X$ અને $M_Y$ છે, જ્યા $M_X\, = \frac{3}{4} M_Y$ છે. $Y$ માંના દ્રાવણ કરતા $X$ માંના દ્રાવણના બાષ્પદબાણનો સાપેક્ષ ઘટાડો $''m''$ ગણો છે. દ્રાવકતા મોલની સાપેક્ષમાં દ્રાવ્યતા મોલ ખૂબ ઓછા છે. તો $''m''$ નું મૂલ્ય જણાવો.View Solution
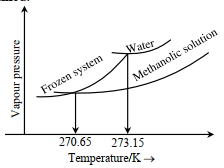
- 5જ્યારે'$x^{\prime} \times 10^{-2} \mathrm{~mL}$ મિથેનોલ (મોલર દળ=32 $\mathrm{g}$; ઘનતા $=0.792 \mathrm{~g} / \mathrm{cm}^3$ ) ને $100 \mathrm{~mL}$ પાણીમાં (ઘનતા $=1 \mathrm{~g} / \mathrm{cm}^3$ ), ઉમેરવામાં આવે છે ત્યારે નીચે મુજબ નો ડાયાગ્રામ પ્રાપ્ત થાય છે.View Solution
$(Image)$
$x=$.. . . . . .(નજીક નો પૂર્ણાક)
[આપેલ : $273.15 \mathrm{~K}$ પર પાણીનો મોલલ ઠારણ બિંદુ અવનયન અયળાંક $1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$ છે]
- 6બે પ્રવાહી $x$ અને $ y,$ આદર્શ બનાવે છે. $300\,K$ તાપમાને $1$ મોલ $x$ અને $ 3$ મોલ $y$ ધરવતા દ્રાવણનું બાષ્પદબાણ $550$ મિમિ છે. તે જ તાપમાને જો $1$ મોલ વધારાનો $y $ દ્રાવણમાં ઉમેરવામાં આવે તો દ્રાવણનું બાષ્પદબાણ $10$ મિમિ જેટલુ વધે છેતો $x$ અને $y$ ના શુધ્ધ અવસ્થામાં બાષ્પદબાણ અનક્રમે ……… મિમિ થાય છે.View Solution
- 7$27\,^oC$ પર $100\, mL$ પાણીમાં $0.6\, g$ યુરીયા (મોલર દળ $= 60\, g\, mol^{-1}$) અને $1.8\, g$ ગ્લુકોઝ (મોલર દળ $= 180\, g\, mol^{-1}$) ઓગળીને એક દ્રાવણ તૈયાર કરવામાં આવ્યુ છે. દ્રાવણનુ અભિસરણ દબાણ .............. $\mathrm{atm}$ જણાવો. $(R = 0.08206\, L\, atm\, K^{-1}\, mol^{-1})$View Solution
- 8$20^{\circ} {C}$ પર બેન્ઝીનનું બાષ્પદબાણ $70$ ટોર અને મિથાઈલ બેન્ઝીનનું $20$ ટોર છે. $20^{\circ} {C}$ પર બાષ્પના તબક્કામાં બેન્ઝીનનો મોલઅંશ બેન્ઝીન અને મિથાઈલ બેન્ઝિનના સમકક્ષ મિશ્રણ ઉપર $.....\,\times 10^{-2}$ (નજીકના પૂર્ણાંકમાં)View Solution
- 9કયાને $ A$ માંથી $B$ દ્રાવણમાં અભિસરણ થતું નથી?View Solution
- 10પાણી માટે $K_f = 1.86\,\, K\,kg\,mol$ $^{-1}$ જો તમારૂં વાહનનું રેડીયેટર $1.0$ કિ. ગ્રામ પાણી ધરાવે તો દ્રાવણ નું ઠારણ બિંદુ $ -2.8\,^o$ સે. જેટલું ઘટાડવામાં માટે ........ $gm$ ઇથીલીન ગ્લાયકોલ $(C_2H_6O_2)$ ઉમેરવામાં આવે છે.View Solution
