$p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલનું કેન્દ્ર ઉદ્ગમબિંદુ પર રહે તે રીતે $x$-અક્ષ પર મૂકેલ છે.ડાયપોલના કેન્દ્રથી અમુક અંતરે આવેલા બિંદુને જોડતી રેખાએ $x$-અક્ષ સાથે બનાવેલો ખૂણો $\theta $ છે.તો તે બિંદુએ વિદ્યુતક્ષેત્રએ $x$-અક્ષ સાથે કેટલો ખૂણો બનાવે? [ $\tan \alpha = \frac{1}{2}\tan \theta $ ]
Medium
c
(c) An electric dipole of moment \(=\bar{p}\)
(c) An electric dipole of moment \(=\bar{p}\)
electric field \(x-\) axis at a point \(=p\)
angle \(=\theta\) with \(x-\) axis
\(\tan a=\frac{1}{2} \tan \theta\)
\((\theta+\alpha)=\) the value of the position vector makes an angle \(\theta\)
\(\theta=60^{\circ}+\alpha\)
now resolving \(E\) into its components
\(E \cos \alpha=\frac{2 p \cos 60^{0}}{4 \pi \epsilon_{0} r^{3}} \quad \longrightarrow(1)\)
\(E \sin \alpha=\frac{p \sin 60^{0}}{4 \pi \epsilon_{0} r^{3}} \quad \longrightarrow(2)\)
Dividing \(2\) by \(1\)
\(\tan \alpha=\frac{1}{2} \tan \theta\)
\(\tan \alpha=\tan (\theta+\alpha)\)
\(\alpha=\theta+\alpha\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2 L \times 2 L \times L$ પરિણામાણ ધરાવતા લંબધનમાં $4 L ^2$ ક્ષેત્રફળ ધરાવતા પૃષ્ઠ $s$ ના કેન્દ્રસ્થાને વિદ્યુતભાર $q$ મૂકવામાં આવે તો $s$ ના સામેના પૃષ્ઠમાંથી પસાર થતું ફલફસView Solution
- 2$4.9 \times 10^{5} \;N / C$ મૂલ્ય ધરાવતું શિરોલંબ વિદ્યુતક્ષેત્ર, $0.1 \,g$ દળ ધરાવતા પાણીના બુંદને નીચે પડતું આટકાવવા પૂરતું છે. બુંદ પરનો વિધુતભાર........$ \times 10^{-9} \;C$ હશેView Solution
[$g =9.8 \,m / s ^{2}$ આપેલા ]
- 3$R$ ત્રિજ્યા ધરાવતી પાતળી તકતીની વિજભાર ઘનતા $\sigma $ છે. તકતીના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર $\frac{\sigma }{{2\,{ \in _0}}}$ છે.કેન્દ્ર આગળ રહેલ ક્ષેત્રની સાપેક્ષમાં કેન્દ્રથી $R$ અંતરે રહેલ અક્ષ પર વિદ્યુતક્ષેત્ર ....View Solution
- 4$R$ ત્રિજયાવાળી પોલી સપાટીમાં $Q$ કુલંબ વિદ્યુતભાર રહેલો છે. જો સપાટીની ત્રિજયા બમણી કરતા સપાટી સાથે સંકળાયેલ ફલક્સ .....View Solution
- 5$1\ gm$ દળના ઘન ગોળામાં $5 \times 10^{21}$ પરમાણુ છે, $0.01\%$ પરમાણુ દીઠ એક ઇલેકટ્રોન દૂર કરતાં ગોળો કેટલા .....$C$ વિદ્યુતભાર પ્રાપ્ત કરે?View Solution
- 6બે બિંદુવત વિદ્યુતભારો $q_2$ = $3 \times 10^{-6}\ C$ અને $q_1$ =$ 5 \times 10^{-6}\ C$ એ $B \,(3, 5, 1)\ m $ આગળ અને $A\, (1, 3, 2)\ m$ આવેલા છે. $q_2$ ના લીધે $q_1$ પર બળનું મૂલ્ય શોધો.View Solution
- 7ઉગમબિંદુ પર કેન્દ્ર રહે તેમ વિધુતડાઇપોલ $x$-અક્ષ પર મુકેલ છે. $OP$ રેખા $x$-અક્ષ સાથે $\frac{\pi }{3}$ખૂણો બનાવે છે.જો $P$ બિદું આગળ વિધુતક્ષેત્ર $x$-અક્ષ સાથે બનાવેલ ખૂણો $\theta$ હોય તો $\theta$=______View Solution
- 8$\overrightarrow{ p }$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલના કેન્દ્રથી $r$ અંતરે વિષુવવૃતીય સમતલ પર રહેલા બિંદુ આગળ વિધુતક્ષેત્ર ........... મળે ($r >>$ ડાઈપોલના બે વિધુતભાર વચ્ચેનું અંતર,$\varepsilon_{0}$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
- 9આકૃતિમાં દર્શાવ્યા અનુસારે બે બિંદુવત વિદ્યુતભારો $- q$ અને $+q$ ને $L$ જેટલા અંતરે મુકવામાં આવેલ છે.View Solution
$R ( R > > L )$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતાનું મૂલ્ય $.....$ પ્રમાણે બદલાશે.
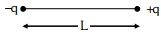
- 10ઋણ વિદ્યુતભાર ધરાવતા ટીપાને ગુરૂત્વાકર્ષણની વિરૂધ્ધ શિરોલંબ $100\ V m^{-1}$ જેટલુ વિદ્યુતક્ષેત્ર આપીને પડતા અટકાવવામાં આવે છે જો ટીપાંનું વજન $1.6 \times 10^{-3}\ g$ હોય તો ટીપામાં સમાયેલ ઇલેક્ટ્રોનની સંખ્યા....View Solution
