$P\,\, = \,\,{\rm{Q}}\,\, = \,\,{\rm{R}}$ જો $\mathop {\,{\rm{P}}}\limits^ \to \,\, + \;\,\mathop {\rm{Q}}\limits^ \to \,\, = \,\,\mathop {\rm{R}}\limits^ \to \,$ હોય તથા $\mathop {\rm{P}}\limits^ \to $ અને $\mathop {\rm{R}}\limits^ \to $ વચ્ચેનો ખૂણો ${\theta _1}$ છે. જો $\mathop {\rm{P}}\limits^ \to \,\, + \;\,\mathop {\rm{Q}}\limits^ \to \,\, + \,\,\mathop {\rm{R}}\limits^ \to \,\, = \,\,\mathop {\rm{0}}\limits^ \to $ હોય તો $\mathop {\rm{P}}\limits^ \to $ અને $\mathop {\rm{R}}\limits^ \to $ વચ્ચેનો ખૂણો ${\theta _2}$ છે. ${\theta _1}$ અને ${\theta _2}$ વચ્ચેનો સંબંધ શું કહે ?
Diffcult
Download our app for free and get started
b
\(P\,\, = \,\,Q\,\, = \,\,R\)
\(P\,\, = \,\,Q\,\, = \,\,R\)
\(\mathop {\,{\rm{P}}}\limits^ \to \,\, + \,\,\mathop {\,{\rm{Q}}}\limits^ \to \, = \,\,\mathop {\,{\rm{R}}}\limits^ \to \,\, \Rightarrow \,\mathop {\,{\rm{P}}}\limits^ \to \,\, - \,\,\mathop {\,{\rm{R}}}\limits^ \to \,\, = \,\, - \mathop {\,{\rm{Q}}}\limits^ \to \)
\({P^2}\,\, + \,\,{R^2}\,\, - \,\,2PR\cos {\theta _1}\,\, = \,\,{Q^2}\, \Rightarrow \,\,2\cos {\theta _1}\,\, = \,\,1\,\, \Rightarrow \,\,{\theta _1}\,\, = \,\,60^\circ \)
હવે \(\mathop {\,{\rm{P}}}\limits^ \to \,\, + \,\,\mathop {\,{\rm{Q}}}\limits^ \to \, + \mathop {\,{\rm{R}}}\limits^ \to \,\, = \,\,0\,\, \Rightarrow \,\,\mathop {\,{\rm{P}}}\limits^ \to \,\, + \,\mathop {\,{\rm{R}}}\limits^ \to \, = \,\, - \,\mathop {\,{\rm{Q}}}\limits^ \to \,\)
\( \Rightarrow {P^2}\,\, + \;\,{R^2}\,\, + \,\,2PR\cos {\theta _2}\,\, = \,\,{Q^2}\)
\( \Rightarrow \,\,\cos {\theta _2}\,\, = \,\, - \frac{1}{2}\,\, \Rightarrow \,\,{\theta _2}\,\, = \,\,120^\circ \) \( \Rightarrow \,\,{\theta _2}\,\, = \,\,2{\theta _1}\,\, \Rightarrow \,\,{\theta _2}\,\, = \,\frac{{{\theta _2}}}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $\vec{P}+\vec{Q}=\overrightarrow{0}$, જો હોય તો નીચેના માંથી ક્યું સાયું છે ?View Solution
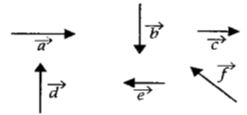
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે ત્રણ સદિશોનો સરવાળો શૂન્ય છે. $\mathop {OB}\limits^ \to \,\,{\text{& }}\,\,\mathop {OC}\limits^ \to $ સદીશનું મૂલ્ય શું હશે ?View Solution
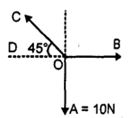
- 3વિધાન $I:$ જો ત્રણ બળો $\vec{F}_{1}, \vec{F}_{2}$ અને $\vec{F}_{3}$ ને ત્રિકોણની ત્રણ બાજુ વડે દર્શાવવામાં આવે છે અને $\overrightarrow{{F}}_{1}+\overrightarrow{{F}}_{2}=-\overrightarrow{{F}}_{3}$ હોય, તો આ ત્રણ બળો સમવર્તી બળો અને તે સમતોલન સ્થિતિને સંતોષે છે.View Solution
વિધાન $II:$ $\overrightarrow{{F}}_{1}, \overrightarrow{{F}}_{2}$ અને $\overrightarrow{{F}}_{3}$ બળો ત્રિકોણની બાજુ હોય, તો તે સમાન ક્રમમાં હોય, તો તે રેખીય સમતોલન સ્થિતિને સંતોષે છે.
ઉપર આપેલા વિધાનો માટે નીચેમાંથી યોગ્ય વિકલ્પ પસંદ કરો.
- 4જો $ 0.5\hat i + 0.8\hat j + c\hat k $ એકમ સદિશ હોય, તો $c$ નું મૂલ્ય કેટલું હશે?View Solution
- 5$\vec A$ અને $\vec B$ નો પરિણામી $\vec A$ સાથે $\alpha $ ખૂણો બનાવે છે. અને $\vec B$ સાથે $\beta $ ખૂણો બનાવે તો .....View Solution
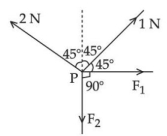
- 6આકૃતિમાં દર્શાવ્યા અનુસાર બિંદુ $P$ આગળ ચાર બળો લાગે છે બળ $F _1$ અને $F _2$ નો ગુણોત્તર $1: x$ હોય તો $x=........$ થશે.View Solution
- 7ત્રણ કણ ${P}, {Q}$ અને ${R}$ અનુક્રમે સદીશ ${A}=\hat{{i}}+\hat{{j}}, {B}=\hat{{j}}+\hat{{k}}$ અને ${C}=-\hat{{i}}+\hat{{j}}$ ની દિશામાં ગતિ કરે છે. તે એક બિંદુ પર અથડાય છે અને જુદી જુદી દિશામાં ગતિ કરે છે. હવે કણ $P$ એ સદીશ $\vec{A}$ અને $\vec{B}$ ને સમાવતા સમતલને લંબ ગતિ કરે છે. તેવી જ રીતે કણ $Q$ એ સદીશ $\vec{A}$ અને $\vec{C}$ ને સમાવતા સમતલને લંબ ગતિ કરે છે. કણ $P$ અને $Q$ ની ગતિની દિશા વચ્ચેનો ખૂણો $\cos ^{-1}\left(\frac{1}{\sqrt{x}}\right)$ છે. તો $x$ નું મૂલ્ય કેટલું હશે?View Solution
- 8જો $ |\overrightarrow A \times \overrightarrow B |\, = \,|\overrightarrow A \,.\,\overrightarrow B |, $ હોય તો $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચે ખૂણો ........ $^o$ હશે.View Solution
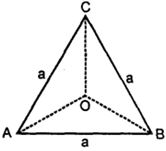
- 9$ABC$ એ સમબાજુ ત્રિકોણ છે. દરેક બાજુની લંબાઈ $'a'$ અને તેનું પરિકેન્દ્ર $O$ છે. તો $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=.......$View Solution
- 10$\overrightarrow{a}$ થી $\overrightarrow{f}$ સુધીના છ સદિશોના મૂલ્યો અને દિશાઓ આકૃતિમાં દર્શાવેલા છે. નીચેનામાંથી કયું વિધાન તેમના વિશે સાચું છે?View Solution
