પાણીનું એક નાનું બિંદુ $h$ ઊંચાઈએેથી સ્થિર અવસ્થામાંથી મુક્ત પતન કરે છે. તેનો અંતિમ વેગ એ
Medium
Download our app for free and get started
d
(d)
(d)
Since drop is falling from a large height it achieves its terminal velocity and then there is no further increase in velocity so \(v\) is independent of ' \(h\) ' if ' \(h\) ' is very large.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
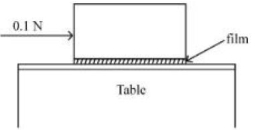
- 1આકૃતિમાં દર્શાવ્યા અનુસાર $0.20\,m ^2$ ના બેઝ (તળીયા) નું ક્ષેત્રફળ ધરાવતા એક ધાતુના ચોસલાને ટેબલ ઉપર મૂકવામાં આવેલ છે. એક $0.25\,mm$ ની પ્રવાહીની કપોટીને બ્લોક (ચોસલું) અને ટેબલની વચ્યે દાખલ કરવામાં આવે છે. બલોકને $0.1\,N$ ના સમક્ષિતિજ બળ વડે ખેંચવામાં આવે છે અને તે અચળ ઝડપથી ગતિ કરે છે. જો પ્રવાહીની સ્નિગ્ધતા $5.0 \times 10^{-3}\;Pa-s$ હોય તો બ્લોકની ઝડપ (લગભગ) $...........\times 10^{-3}\,m / s$ હશે.View Solution
- 2$\rho$ ઘનતાના પ્રવાહીને સમાવતું બીકર એ પ્રવેગ $a$ સાથે ઉપર ગતિ કરે છે. પ્રવાહીની સપાટીથી $h$ ઊંંડાઈએ પ્રવાહીને લીધે લાગતું દબાણ કેટલું છે ?View Solution
- 3$\sigma$ સાપેક્ષ ધનતા ધરાવતા એક ગોળાનો વ્યાસ $D$ છે અને તેને $d$ વ્યાસનો સમકેન્દ્રિય પોલાણ઼ (ખાડો) છે. જો તે ટેન્કમાંના પાણી પર તરી શકે તે માટે $\frac{\mathrm{D}}{\mathrm{d}}$ ગુણોત્તર ............ છે.View Solution
- 4વરસાદના ટીપાનું દળ $3.0\times10^{-5}\, kg$ અને સરેરાશ ટર્મિનલ વેગ $9\, m/s$ છે. આ ટીપાં દ્વારા પ્રતિ દર વર્ષે $100\, cm$ વરસાદ મેળવતી $1\,cm^2$ સપાટી પર કેટલી ઉર્જા મેળવાશે?View Solution
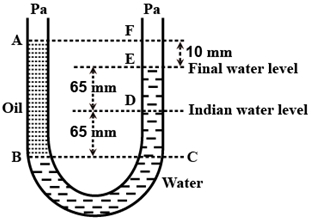
- 5એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution
- 6View Solutionએક બરફનો બ્લોક એ એવા પ્રવાહીમાં તરે છે જેની ઘનતા પાણી કરતા ઓછી છે. બ્લોકનો અમુક ભાગ પ્રવાહીની બહાર રહે છે, જ્યારે તે પુરેપુરો પીગળી જાય, તો પ્રવાહીનું લેવલ
- 7એક પ્રેશર-પંપ (ડંકી)ને પાણી બહાર લાવવા માટે $10\,cm ^2$ આડછેદ ધરાવતી એક સમક્ષિતિજ નળી છે. જેમાંથી $20\,m / s$. ની ઝડપથી પાણી બહાર નીકળે છે. નળીની સામે રહેલી દિવાલ સાથે અથડાઈને નળીમાંથી સમક્ષિત દિશામાં બાર નીકળતું પાણી અટકી જાય છે. દિવાલ પર લાગતું બળ $......\,N$ હશે.[પાણીની ધનતા : = $1000\,kg / m ^3$ આપેલ છે.]View Solution
- 8એક તળાવની સપાટીથી $10 \,m$ ઊંડાઈએ રહેલા તરવૈયા પર દબાણ ($atm$ માં) કેટલું હશે ?View Solution
- 9એક નિયમિત આડ-છેદની શિરોલંબ $U-$ટ્યૂબએે બંને ભૂજામાં પાણી ધરાવે છે. કોઈ પણ એક ભૂજા પર $10 \,cm$ ની ગ્લિસરીન સ્તંભ ઉમેરવામાં આવે છે. ($R.D. = 1.2$) બંને ભૂજામાં બંને મુક્ત સપાટીઓ વચ્ચેના સ્તરનું તફાવત ........ $cm$ હશે ($R.D =$ સાપેક્ષ ધનતા)View Solution
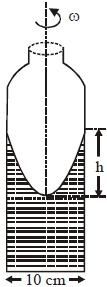
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે એક નળાકાર પાત્રમાં પ્રવાહી ભરીને તેને પોતાની અક્ષને અનુલક્ષીને ફેરવવામાં આવે છે. પાત્રની ત્રિજ્યા $5\, cm$ અને ભ્રમણની કોણીય ઝડપ $\omega\; rad \,s^{-1}$ છે. પાત્રની વચ્ચે અને પાત્રની સપાટી વચ્ચે ઊંચાઈનો ફેરફાર $h($ $cm$ માં)કેટલો હશે?View Solution
