પદાર્થને સમક્ષીતિજ સાથે $30^o$ ના ખૂણે $30\, m/s$ ના વેગથી ફેકવામાં આવે તો $1\, sec$ પછી તેનો વેગ કેટલો થાય?
Medium
a
Horizontal component of velocity along \(x\)-axis after \(1 s\) is
Horizontal component of velocity along \(x\)-axis after \(1 s\) is
\(v _{ x }= u _{ x }+ gt\)
\(v _{ x }= u \cos \theta+0 \times 1\)
\(v _{ x }=30 \cos 30^{\circ}\)
\(v _{ x }=15\sqrt3\; m / s\)
Vertical component of the velocity along \(y\)-axis after \(1 s\) is
\(v _{ y }= u _{ y }- gt\)
\(v _{ y }=30 \sin 30^{\circ}-10 \times 1\)
\(v _{ y }=15-10\)
\(v _{ y }=5 m / s\)
Velocity of a body after 1 s is
\(\overrightarrow{ v }= v _{ x } \hat{ i }+ v _{ y } \hat{ j }\)
\(\overrightarrow{ v }=15\sqrt3 \hat{ i }+5 \hat{ j }\)
Magnitude, \(v =|\overrightarrow{ v }|=\sqrt{(15\sqrt3)^{2}+(5)^{2}}\)
\(v =\sqrt{700}\)
\(v =10 \sqrt{7}\; m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વર્તુળના પરિધ પર ગતિ કરતી વસ્તુનો કોણીય પ્રવેગ $.......$ હોય છે.View Solution
- 2બોલને $10m$ ઊચાઇ વાળા મકાન પરથી $10\, m/s$ ના વેગથી સમક્ષિતીજ સાથે $30^o$ ખૂણે ફેકવામા આવે તો બોલ જયારે $10\;m$ ની ઊચાઇએ પહોંચે ત્યાં સુઘીમાં તેણે કેટલું અંતર ($m$ માં)કાપ્યું હશે?View Solution
$(g \,= \,10 m/s^2, \,sin \,30^o \,= \,\frac{1}{2}$, $\cos \,{30^o}\, = \,\frac{{\sqrt 3 }}{2}$)
- 3$15^o$ ના ખૂણે $u$ વેગથી ફેંકેલા પદાર્થની અવધિ $R$ છે.તો તે પદાર્થને $45^o$ ના ખૂણે $2u$ વેગથી ફેંકતા પદાર્થની અવધિ કેટલી મળે?View Solution
- 4${m_1}$ અને ${m_2}$ દળની બે કાર ${r_1}$ અને ${r_2}$ ત્રિજયામાં પરિભ્રમણ કરે છે. બંને કાર સમાન સમય $t$ માં પરિભ્રમણ પૂરું કરે છે. કારની કોણીય ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
- 5$ t= 0$ સમયે, સમક્ષિતિજ સાથે $60^o$ ના ખૂણે એક પદાર્થને $10\, ms^{-1}$ ગતિથી પ્રક્ષેપિત કરવામાં આવે છે. $t=1\,s$ પર તેના ગતિપથની વક્રતા ત્રિજ્યા $R$ છે. હવાનો અવરોધ અવગણતાં અને ગુરૂત્વપ્રવેગને $g=10\, ms^{-2}$ લેતા $R$ નું મૂલ્ય ........ $m$ હશે.View Solution
- 6એક પદાર્થનું કોણીય સ્થાનાંતર $(\theta ) = 2{t^3} + 0.5$,તો પદાર્થનો કોણીય વેગ $2 \,sec$ સમયે ......... $rad/sec$ હશે.View Solution
- 7કોઈ રાઇફલમાંથી છૂટેલી ગોળીની પ્રારંભિક ઝડપ $630\, m/s$ છે. લક્ષ્યની ક્ષિતિજ પર તેનાથી $700\, m$ દૂર લક્ષ્યના કેન્દ્ર પર રાઇફલને ફાયર કરવામાં આવે છે. લક્ષ્યને તાકવા માટે રાઈફલને લક્ષ્યના કેન્દ્રથી કેટલી ઉપર ($m$ માં) રાખવી જોઈએ? ($g=10 \;m/s^2$ લો)View Solution
- 8એક કણ ગતિની શરૂઆત કરીને $r$ ત્રિજયાના વર્તુળમાં ગતિ કરે છે.તે તેના $n$ માં પરિભ્રમણ દરમિયાન $\mathrm{V}_{0} \;\mathrm{m} / \mathrm{s}$ વેગ પ્રાપ્ત કરે છે.તો તેનો કોણીય પ્રવેગ કેટલો હશે?View Solution
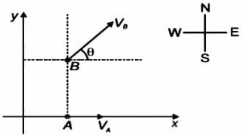
- 9આકૃતિમાં બે જહાજો $x-y$ સમતલમાં $V_A$ અને $V_B$ વેગ સાથે ગતિ કરી રહ્યા છે. જહાજો એવી રીતે ગતિ કરી રહ્યા છે જેથી $B$ હમેશા $A$ ના ઉત્તરમાં રહે.તો $\frac{V_A}{V_B}$ નો ગુણોત્તર શું થશે ?View Solution
- 10$m$ દળ ધરાવતો એક પદાર્થ અચળ ઝડપ સાથે $R$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ગતિ કરે છે તેના પર અચળ મૂલ્યનું $F$ બળ લાગે છે. તો પદાર્થની ગતિ ઉર્જા કેટલી થાય ?View Solution
