પ્લેટનું ક્ષેત્રફળ $A$ એને બે પ્લેટ વચ્ચેનું અંતર $d$ ધરાવતું સમાંતર પ્લેટ કેપેસિટર ડાઇલેક્ટ્રિકથી ભરેલું છે. કેપેસિટરની ક્ષમતા શું હશે જ્યારે ડાઇલેક્ટ્રિકની પરમિટિવિટી નીચે પ્રમાણે બદલાય.
$\varepsilon(x)=\varepsilon_{0}+k x, \text { for }\left(0\,<\,x \leq \frac{d}{2}\right)$
$\varepsilon(x)=\varepsilon_{0}+k(d-x)$, for $\left(\frac{d}{2} \leq x \leq d\right)$
JEE MAIN 2021, Diffcult
b
Taking an element of width \(dx\) at a distance \(x(x < d / 2)\) from left plate
Taking an element of width \(dx\) at a distance \(x(x < d / 2)\) from left plate
\(dC =\frac{\left(\varepsilon_{0}+ kx \right) A }{ dx }\)
Capacitance of half of the capacitor
\(\frac{1}{C}=\int_{0}^{ d / 2} \frac{1}{ dc }=\frac{1}{ A } \int_{0}^{ d / 2} \frac{ dx }{\varepsilon_{0}+ kx }\)
\(\frac{1}{ C }=\frac{1}{ kA } \ln \left(\frac{\varepsilon_{0}+ kd / 2}{\varepsilon_{0}}\right)\)
Capacitance of second half will be same
\(C _{\text {eq }}=\frac{ C }{2}=\frac{ kA }{2 \ln \left(\frac{2 \varepsilon_{0}+ kd }{2 \varepsilon_{0}}\right)}\)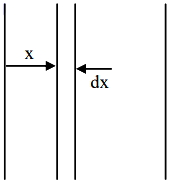
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હવામાં ગોળાકારની કેપેસિટિ $50 \,\mu F$ છે. અને તેને તેલમાં ડૂબડતાં તે બને $110 \,\mu F$ છે. તો તેલનો ડાઈ ઈલેકટ્રીક ગણો.View Solution
- 2જો આ ક્ષેત્રનું સ્થિતિમાન $x, y$ યામને આધારે $V=10\,axy$ થી દર્શાવતું હોય તો વિદ્યુતક્ષેત્રની તિવ્રતાનો સદિશ કયો ગણાશે?View Solution
- 3જો ${q}_{{f}}$ એ કેપેસિટર પ્લેટો પરનો મુક્ત વિદ્યુતભાર અને ${q}_{{b}}$ એ કેપેસિટર વચ્ચે મૂકવામાં આવેલા ડાઇલેક્ટ્રિક અચળાંક $k$ ના ડાઇલેક્ટ્રિક ચોચલા પરનો બાઉન્ડ ચાર્જ હોય, તો બાઉન્ડ ચાર્જ $q_{b}$ ને કઈ રીતે દર્શાવાય?View Solution
- 4ચાર સમાન વિદ્યુતભારો $Q$ ને $xy$ સમતલમાં $(0, 2), (4, 2), (4, -2)$ અને $(0, - 2)$ બિંદુઓ પર મુકવામાં આવેલ છે. આ તંત્રના ઉગમ બિંદુ પર પાંચમા વિધુતભાર $Q$ ને મુકવા જરૂરી કાર્ય ________ છે.View Solution
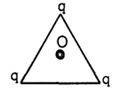
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણે સમબાજુ ત્રિકોણના ત્રણેય ખૂણા પર ત્રણ સમાન વિદ્યુતભારો મૂકેલા છે. નીચના પૈકી (સામાન્ય નામકરણ) કેન્દ્ર આગળ $E$ અને $V$ માટે કયું વિધાન સાચું છે.View Solution
- 6View Solutionવિદ્યુત ડાઈપોલને લીધે આપેલ બિંદુ આગળ વિદ્યુત સ્થિતિમાન ....... હશે.
- 7બે સમકેન્દ્રિય ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે, ${R_1}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_1}$ અને ${R_2}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_2}$ છે,તો કેન્દ્રથી $x$ અંતરે આવેલા બિંદુએ વોલ્ટેજ કેટલો થાય? (${R_2} > x > {R_1}$)View Solution
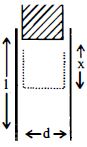
- 8$l$ લંબાઈ અને $w$ જાડાઈ ધરાવતી પ્લેટમાંથી સમાંતર પ્લેટ કેપેસીટર બનાવવામાં આવે છે. જેમાં બે પ્લેટને એકબીજાથી $d$ અંતરે રાખવામા આવે છે. એક $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતો બ્લોક તેની વચ્ચે બરાબર ફિટ થાય તે રીતે પ્લેટની ધારની નજીક મૂકેલો છે. તેને કેપેસીટરની અંદર $F = -\frac{{\partial U}}{{\partial x}}$ જેટલા બળથી ખેચવામાં આવે છે, જ્યાં $U$ એ જ્યારે ડાઈઇલેક્ટ્રિક કેપેસીટરની અંદર $x$ અંતર જેટલો હોય ત્યારની કેપેસીટરની ઉર્જા છે. જો $Q$ એ કેપેસીટર પરનો વિજભાર હોય તો જ્યારે ડાઈઇલેક્ટ્રિક અચળાંકવાળો બ્લોક પ્લેટની ધારની નજીક હોય ત્યારે તેના પર કેટલું બળ લાગતું હશે?View Solution
- 9બે સંઘારકો $C _{1}$ અને $C _{2}$ ને આકૃતિમાં દર્શાવ્યા અનુસાર જોડવામાં આવેલા છે. પ્રારંભમાં સંધારક $C _{1}$ ને $V$ વોલ્ટના સ્થિતિમાન તફવત થી બેટરી વડે વિદ્યુતભારિત કરવામાં આવે છે. હવે બેટરી દ્દૂર કરવામાં આવે છે અને આ રીતે વિદ્યુતભારિત $C_{1}$ સંધારકને કળ $S$ બંધ કરીને અવીજભારિત $C_{2}$ સંધારક સાથે જોડવામાં આવે છે. સંતુલન સ્થિતિ મેળવ્યા બાદ સંધારક $C _{2}$ પરનો વીજભાર ........ થશે.View Solution
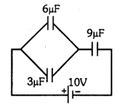
- 10$6\, \mu F, 3\, \mu F$ અને $9\, \mu F$ મૂલ્ય ધરાવતા ત્રણ કેપિસિટરોને આકૃતિ મુજબ જોડેલા છે. અને આ સંયોજનને $10$ વોલ્ટની બેટરી સાથે જોડવામાં આવે છે. $9\, \mu F$ કેપિસિટરની પ્લેટો વચ્ચેનો સ્થિતિમાન તફાવત કેટલા ......$V$ હશે ?View Solution