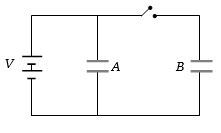
પ્રથમ કળ બંધ કરવામાં આવે છે,હવે કળ ખુલ્લી કરીને બંને કેપેસિટરમાં ડાઇઇલેકિટ્રક $3$ ભરતાં તંત્રની પહેલાની અને પછીની ઊર્જાનો ગુણોત્તર કેટલો થાય?

IIT 1983, Diffcult
c
(c) Initially potential difference across both the capacitor is same hence energy of the system is
\({U_1} = \frac{1}{2}C{V^2} + \frac{1}{2}C{V^2} = C{V^2}\)\(……(i)\)
In the second case when key \(K\) is opened and dielectric medium is filled between the plates, capacitance of both the capacitors becomes \(3C\), while potential difference across \(A\) is \(V\) and potential difference across \(B\) is \(\frac{V}{3}\) hence energy of the system now is
\({U_2} = \frac{1}{2}\,(3C){V^2} + \frac{1}{2}\,(3C)\,{\left( {\frac{V}{3}} \right)^2}\)\( = \frac{{10}}{6}\,C{V^2}\)\(……(ii)\)
So, \(\frac{{{U_1}}}{{{U_2}}} = \frac{3}{5}\)
(c) Initially potential difference across both the capacitor is same hence energy of the system is
\({U_1} = \frac{1}{2}C{V^2} + \frac{1}{2}C{V^2} = C{V^2}\)\(……(i)\)
In the second case when key \(K\) is opened and dielectric medium is filled between the plates, capacitance of both the capacitors becomes \(3C\), while potential difference across \(A\) is \(V\) and potential difference across \(B\) is \(\frac{V}{3}\) hence energy of the system now is
\({U_2} = \frac{1}{2}\,(3C){V^2} + \frac{1}{2}\,(3C)\,{\left( {\frac{V}{3}} \right)^2}\)\( = \frac{{10}}{6}\,C{V^2}\)\(……(ii)\)
So, \(\frac{{{U_1}}}{{{U_2}}} = \frac{3}{5}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\vec p$ મોમેન્ટ ધરાવતી એક વિદ્યુત ડાઇપોલને વિદ્યુતક્ષેત્ર $\vec E$ ની દિશામાં મૂકેલો છે.આ ડાઇપોલને $90 ^o $ ના કોણે ભ્રમણ કરાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 2$X-Y$ યામ પદ્ધતિના ઉગમબિંદુ $(0, 0)$ આગળ $10^{-3}\ \mu C$ નો એક વિદ્યુતભાર મૂકેલો છે. બે બિંદુઓ $A$ અને $B$ $(\sqrt 2 ,\,\,\sqrt 2 )$ અને $(2, 0)$ આગળ ગોઠવેલા છે. બિંદુ $A$ અને $B$ વચ્ચેનો સ્થિતિમાનનો તફાવત .......$V$ હશે.View Solution
- 3સમાંતર પ્લેટ કેપેસીટરની બે પ્લેટ વચ્ચે ડાઈઇલેક્ટ્રિક પદાર્થ નથી પરતું તેમની વચ્ચેનું અંતર $0.4 \,cm$ છે તેનું કેપેસીટન્સ $2\,\mu \,F$ છે. હવે બે પ્લેટ વચ્ચેનું અંતર ઘટાડીને અડધું અને તેમની વચ્ચે $2.8$ ડાઈઇલેક્ટ્રિકનું મૂલ્ય ધરાવતો પદાર્થ મૂકવામાં આવે તો તેનું નવું કેપેસીટન્સ કેટલા $\mu \,F$ મળે?View Solution
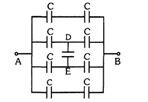
- 4આપેલ આકૃતિમાં પરિણામી કેપેસિટન્સ $C_{AB}$ =......$C$View Solution
- 5એક $0.2 \, \mu F$ કેપેસિટન્સ વાળા કેપેસિટરને $600\, V$ વોલ્ટેજે વિદ્યુતભારિત કરેલ છે. બેટરીને દૂર કર્યા બાદ, તેને $1.0\ \mu F$ ના કેપેસિટર સાથે સમાંતરમાં જોડવામાં આવે છે, ત્યારે કેપેસિટરનો સ્થિતિમાન.........$V$ હશે.View Solution
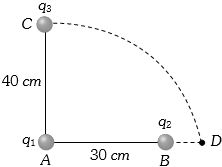
- 6આકૃતિમાં દર્શાવ્યા મુજબ be $q_1$ અને $q_2$ વિદ્યુતભાર $30\;cm$ અંતરે છે. ત્રીજો વિદ્યુતભાર $q_3$ ને $C$ થી $D$ સુધી $40 \;cm$ ત્રિજ્યાના વર્તુળની ચાપ પર લઇ જવામાં આવે છે. તંત્રની સ્થિતિઊર્જામા $\frac{{{q_3}}}{{4\pi {\varepsilon _0}}}k$ ફેરફાર થાય તો, $k=$View Solution
- 7ઉગમબિંદુથી $R_o$ અંતરે એક સમાન ગોલીય સંમિતિ ધરાવતી પૃષ્ઠ વિધુતભાર ઘનતા રહેલ છે. વિદ્યુતભાર વિતરણ પ્રારંભમાં સ્થિર છે, અને પછી તેનું પરસ્પર અપાકર્ષણ થવાને કરાણે સમાન રીતે વિસ્તરણ થાય છે. વિસ્તરણ માટે તેની તત્ક્ષણિક ત્રિજ્યા $R(t)$ ના વિધેય તરીકે ઝડપ $V(R(t))$ ને રજુ કરતી આકૃતિ નીચેનામાથી કઈ છે.View Solution
- 8$R_{1}$ અને $\mathrm{R}_{2}$ ત્રિજ્યા ધરાવતા બે વિદ્યુતભારિત ગોળાકાર સુવાહકોને એક તારથી જોડવામાં આવેલા છે. તો ગોળાઓની પૃષ્ઠ વિદ્યુતભાર ઘનતાઓનો ગુણોત્તર $\left(\sigma_{1} / \sigma_{2}\right)$ $.....$ છે.View Solution
- 9View Solutionસમાન વિદ્યુતક્ષેત્રમાં વિદ્યુત ડાઈપોલ માટે ન્યૂનત્તમ સ્થિતિ ઊર્જાની શરત ...... છે.
- 10View Solutionવિદ્યુતભારની ધ્રુવીભવનનો સિધ્ધાંત કોણે સાબિત કર્યો હતો?
