$R$ ત્રિજયા અને $M$ દળ ધરાવતી એક નિયમિત વર્તુળાકાર તકતીને લંબ એવી રીતે તેની ધારમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?
AIPMT 2005,AIPMT 2006, Medium
Download our app for free and get started
a
Moment of inertia of a uniform circular disc about an axis through its centre and perpendicular to its plane is
Moment of inertia of a uniform circular disc about an axis through its centre and perpendicular to its plane is
\(I_{G}=\frac{1}{2} M R^{2}\).
By the theorem of parallel axes,
\(I=I_{G}+M d^{2}=\frac{1}{2} M R^{2}+M R^{2}=\frac{3}{2} M R^{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનિયમિત વર્તૂળગતિ કરતા કણની રેખીય ઝડપ ચાર ગણી કરવામાં આવે અને કોણીય વેગ બમણો કરવામાં આવે, તો કણનો કેન્દ્રગામી પ્રવેગ .....
- 2View Solutionઘન ગોળા માટે ચાકગતિ અને રેખીયગતિ ઊર્જા નો ગુણોત્તર
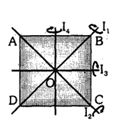
- 3પાતળી ચોરસ પ્લેટ $ ABCD $ ની જાડાઈ નિયમિત છે. તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 4View Solutionએક કણ વર્તુળમાં નિયમિત ઝડપે નીચે દર્શાવ્યા પ્રમાણે પરિભ્રમણ કરી રહ્યોં છે. ઉગમબિંદુના સંદર્ભમાં કણનું કોણીય વેગમાન શું થાય?
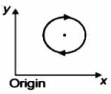
- 5એક ઘન સમાન શંકુના શિરોબિંદુથી દ્રવ્યમાન કેન્દ્રથી અંતર $z_0$ છે.જો તેના આધારની ત્રિજયા $R$ અને ઊંચાઇ $h$ હોય,તો $z_0$ _________ બરાબર થશે.View Solution
- 6આયર્ન માંથી બે પ્લેટ $A$ અને $B$ બનાવેલ છે જેની ત્રિજ્યા અનુક્રમે $r$ અને $4r$ અને જાડાઈ અનુક્રમે $t$ અને $t/4$ છે. $A$ અને $B$ ની જડત્વની ચાકમાત્રા $I_A $ અને $I_B $ હોય તો તેમની વચ્ચેનો સંબંધ .View Solution
- 7સમાન દળ અને જુદી-જુદી ત્રિજ્યાઓ ધરાવતી બે તક્તિઓ કે જે જુદા-જુદા દ્રવ્યોની બનેલી છે તે એવી રીતે બનાવવામાં આવે છે કે જેથી તેની જાડાઈ અનુક્રમે $1\,cm$ અને $0.5\,cm$ હોય. દ્રવ્યની ઘનતાઓ $3:5$ ના ગુણોતરમાં છે. આ તક્તિઓની તેમનાં વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રાઓ $\frac{x}{6}$ નાં ગુણોતરમાં મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution
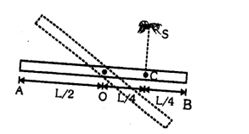
- 8આકૃતિમાં નિયમિત સળિયો $AB $ની લંબાઇ $ L$ અને દળ $M$ છે તેને તેના કેન્દ્ર $ O$ પર એવી રીતે કિલકીત કરેલો છે જેથી શિરોલંબ સમતલમાં મુક્તપણે ભ્રમણ કરી શકે છે. સળિયો પ્રારંભમાં સમક્ષિતિજ સ્થિતિમાં છે તેટલાજ દળ $M $ નું પદાર્થ $S$ શિરોલંબમાંથી $v$ વેગથી $C$ બિંદુ પર પડે છે. $C$ એ $ O$ અને $B$ વચ્ચેનું મધ્યબિંદુ છે. પદાર્થના પતનની તરત જ બાદ સળિયાનો કોણીય વેગ શોધો.View Solution
- 9View Solutionએવી પરિસ્થિતિ લો કે જેમાં એક રિંગ, નક્કર નળાકાર અને નક્કર ગોળો સમતલ ઢાળ પરથી સરક્યા વિના ગબડે છે. ધારો કે તેઓ સ્થિર સ્થિમાંથી શરૂઆત કરે છે અને તેમના વ્યાસ સમાન છે.
આ પરિસ્થિતિ માટે યોગ્ય વિધાન કયું છે
- 10View Solutionઢોળાવવાળા સમતલ પર તકતી સરક્યા વિના ગબડે છે. તો તેની કુલ ઊર્જાનો કેટલામો ભાગ ચાકગતિ ઊર્જા સ્વરૂપે મળશે ?