શુદ્ધ સેમીકન્ડક્ટરમાં ઈલેક્ટ્રોન હોલ જાડકાં \(= 7 × 10^{15 } / m^3, n_{total intial } = n_h + n_e = 14× 10^{15}\)
દાતાર અશુદ્ધિ \({{\text{N}}_{\text{D}}}\, = \,\,\frac{{5\,\, \times \,\,{{10}^{28}}}}{{{{10}^7}}}\,\, = \,\,5\,\, \times \,\,{10^{21}}\,\,\) અને \({n_{e\,}} = \,\,\frac{{{N_D}}}{2}\, = \,\,2.5\,\, \times \,\,{10^{21}}\)
તેથી, \(n_{final} = n_h + n_e ⇒ n_{final} \approx n_e \approx 2.5×10^{21} ( ∵ n_e >> n_h)\)
ઘટક \( = \,\,\frac{{{{\text{n}}_{{\text{final}}}}\,\, - \,\,{n_{initial}}}}{{{n_{initial}}}}\, = \,\,\frac{{2.5\,\, \times \,\,{{10}^{21}}\,\, - \,\,14\, \times \,\,{{10}^{15}}}}{{14\,\, \times \,\,{{10}^{15}}}}\,\, \approx \,\,\frac{{2.5\,\, \times \,\,{{10}^{21}}}}{{14\,\, \times \,\,{{10}^{15}}}}\,\, = \,\,1.8\, \times \,\,{10^5}\)
Download our appand get started for free
Similar Questions
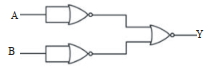
- 1View Solutionનીચે આપેલ પરિપથ માટે, પરિપથ દ્વારા થતું લોજીક કાર્ય (operation) શોધો અને નીચે આપેલા વિકલ્પોમાંથી સાયો વિકલ્પ પસંદ કરો.
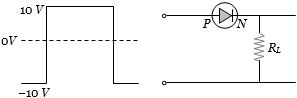
- 2આપેલ પરિપથ માટે અવરોધ $R_L$ વચ્ચેનો વોલ્ટેજ કેટલો થાય?View Solution
- 3રિવર્સ બાયસ $PN$ જંક્શનમાં ડીપ્લીશન સ્તરના મધ્યમાં ...View Solution
- 4$p-n$ જંકશન ડાર્યોડમાં પોટેન્શિયલ બેરિયર ઉત્પન્ન થવાનું કારણView Solution
- 5$N-$ પ્રકારના $Ge $ માં ઈલેક્ટ્રોન્સની મોબિલીટી $5000cm^2/volt sec$ અને વાહકતા $5mho/cm $ છે. જો હોલ્સની અસર અવગણી શકાય એવી હોય તો મિશ્રણના અશુદ્ધતાનું પ્રમાણ કેટલું હશે?View Solution
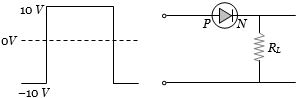
- 6આપેલ પરિપથ માટે અવરોધ $R_L$ વચ્ચેનો વોલ્ટેજ કેટલો થાય?View Solution
- 7નીચે બે વિધાનો આપેલા છેઃ એકને કથન $A$ અને બીજાને કારણ $R$ વડે રજૂ કરેલ છે.View Solution
કથન $A$: પ્રકાશની તીવ્રતા માપવા માટે સામાન્ય રીત ફોટોડાયોડને ફોરવર્ડ-બાયસ સ્થિતિમાં વાપરવામાં આવે છે.
કારણ $R$: $P-n$ જંકશન ડાયોડ માટે, આપેલ વોલ્ટેજ $V$ માટે, ફોરવર્ડ બાયસ સ્થિતિમાં પ્રવાહ રિવર્સ બાયસ સ્થિતિમાં પ્રવાહ કરતાં વધારે હીય છે. જ્યાં| $V _{ z }|>\pm V \geq| V _0 \mid$ અહીયા $v_0$ એ શ્રેસોલ્ડ વોલ્ટેજ અને $v_z$ એ બ્રેકડાઉન વોલ્ટેજ છે.
ઉપરના વિધાનોના સંદર્ભમાં નીચે આપેલા વિકલ્પેમાંથી સૌથી વધુ બંધ બેસતો જવાબ પસંદ કરો.
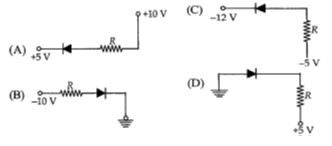
- 8View Solutionનીચે દર્શાવેલ કયા પરિપથમાં ડાયોડ ફોરવર્ડ બાયસ સ્થિતિમાં છે.?
- 9સંપૂર્ણ તરંગ રેક્ટિફાયરમાં જો ઈનપુટ આવૃત્તિ $50 Hz$ હોય અને આઉટપુટ રીપલ આવૃત્તિએ .........$Hz$View Solution
- 10ફોટો સેલમાં રહેલ $PN$ જંકશનમાં એક રંગી પ્રકાશ આપાત કરતાં ઉત્પન્ન થતાં ફોટો વિદ્યુતચાલક બળ ($e.m.f.$) કોના સમપ્રમાણમાં હોય છે?View Solution
