Equation of motion of particle 1 ,
\(x_1=A \sin \left(\omega t+\phi_1\right) \text {...1 }\)
Equation of motion of particle 2,
\(x_2=A \sin \left(\omega t+\phi_2\right) \text {...2 }\)
From (1) and (2)
\(x_2-x_1=A \sin \left(\omega t+\phi_2\right)-A \sin \left(\omega t+\phi_1\right)\)
\(=A\left[\sin \left(\omega t+\phi_2\right)-\sin \left(\omega t+\phi_1\right)\right]\)
Using, \(\sin C-\sin D=2 \cos \left(\frac{C+D}{2}\right) \cdot \sin \left(\frac{C-D}{2}\right)\)
\(x_2-x_1=2 A \cos \left(\omega t+\frac{\phi_1+\phi_2}{2}\right) \cdot \sin \left(\frac{\phi_2-\phi_1}{2}\right)\)
Given that, \(\left(x_0+x_2-x_1\right)_{\max }=x_0+A\)
\(\Rightarrow\left(x_2-x_1\right)_{\max }=A\)
\(\text { To get }\left(x_2-x_1\right)_{\max } \text {, we }\)
\(\Rightarrow 2 A \sin \left(\frac{\phi_2-\phi_1}{2}\right)=A\)
\(\Rightarrow \sin \left(\frac{\phi_2-\phi_1}{2}\right)=\frac{1}{2} \)
\(\Rightarrow \frac{\phi_2-\phi_1}{2}=\frac{\pi}{6} \text { or } \frac{5 \pi}{6}\)
\(\Rightarrow \phi_2-\phi_1=\frac{\pi}{3} \text { or } \frac{5 \pi}{3}\)
\(\text { To get }\left(x_2-x_1\right)_{\max } \text {, we assume } \cos \left(\omega t+\frac{\phi_1+\phi_2}{2}\right)=1\)
Download our appand get started for free
Similar Questions
- 1સમક્ષિતિજ સમતલ ઉપર અને નીચે $1\, cm$ કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે. જો તેના પર રહેલો $10\, kg$ દળનો પદાર્થ તેના સંપર્કમાં રહે તે માટે તેની મહત્તમ આવૃતિ($Hz$) કેટલી હોવી જોઈએ?View Solution
- 2જો સરળ આવર્તગતિ કરતાં પદાર્થનો કંપવિસ્તાર $50\, mm$ અને આવર્તકાળ $2\, sec$ હોય તો તેનો મહત્તમ વેગ ...... $m/s$ હોય.View Solution
- 3સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા સમતોલન સ્થાનથી કંપવિસ્તારના અડધા અંતરે $2.5\, J$ છે,તો કુલઊર્જા કેટલી .... $J$ થાય?View Solution
- 4સમાન કંપવિસ્તાર અને કળાના અચળ તફાવત $\frac{\pi}{4}$ થી બે સરખા લોલક ગતિ કરે છે. જ્યારે એકનો મહત્તમ વેગ $v$ હોય ત્યારે બીજાનો મહત્તમ વેગ કેટલો હશે?View Solution
- 5સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $ X = 7\cos 0.5\pi t $ છે,તો સમતોલન સ્થિતિથી મહત્તમ સ્થાનાંતર પહોંચવા માટે કેટલો ..... $(\sec)$ સમય લાગે?View Solution
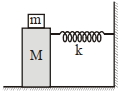
- 6આપેલ આકૃતિમાં, એક $M$ દળ જેનો એક છેડો દઢ આધાર સાથે જડિત કરેલ છે તેવી સમક્ષિતિજ સ્પ્રિંગ સાથે જોડેલ છે. સ્વિંગનો સ્પ્રિંગ અચળાંક $k$ છે. ઘર્ષણરહિત સપાટી પર દળ $T$ જેટલા આવર્તકાળ અને $A$ જેટલા કંપવિસ્તાર સાથે દોલન કરે છે. આકૃતિમાં દર્શાવ્યા અનુસાર, દળ જ્યારે સંતુલન સ્થિતિમાં હોય છે ત્યારે બીજા $m$ દળને ધીરેથી (સાવચેતીથી) તેના પર જોડવામાં આવે છે. દોલનનો નવો કંપવિસ્તાર ............ થશે.View Solution
- 7સરળ આવર્ત ગતિ કરતાં પદાર્થનો કંપવિસ્તાર $4\,cm$ છે,સમતોલન સ્થાન પાસે વેગ $10\,cm/s$ હોય,તો કયાં સ્થાન આગળ વેગ $5 \,cm/s$ થાય?View Solution
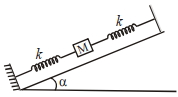
- 8આપેલા આવૃત્તિમાં, $M$ દળ ધરાવતો પદાર્થ બે દળરહિત સ્પ્રિંગો વચ્ચે ઘર્ષણરહિત ઢળતા સમતલ (ઢોળાવ) પર રાખવામાં (બાંધવામાં) આવેલ છે. સ્પ્રિંગોનાં મુક્ત છેડાઓને જડ-આધાર સાથે જોડવામાં આવેલ છે. જે દરેક સ્પ્રિંગનો બળ અચળાંક $k$ હોય તો પદાર્થનાં દોલનની આવૃત્તિ ...... છે.View Solution
- 9સરળ આવર્તગતિ કરતાં કણની ગતિને દર્શાવવા માટે $x=$ $0.01 \sin 100 \pi(t+0.05)$ સમીકરણ વપરાય છે. તેનો આવર્તકાળ ........... $s$ હશે.View Solution
- 10એક સ્પ્રિંગ સાથે જોડેલા અને સરળ આવર્તગતિ કરતા પદાર્થના સ્થાનાંતરનું સમીકરણ $x =2 \times 10^{-2} \cos \pi t$ મીટર છે. પ્રથમ વખત મહત્તમ ઝડપ પ્રાપ્ત કરવા કેટલો સમય ($sec$ માં) લાગશે?View Solution
