$K(x) = K_0 + \lambda x$ ($\lambda =$ અચળાંક)
શૂન્યાવકાશમાં કેપેસીટરનું મૂલ્ય $C_0$ હોય તો $C_0$ના સ્વરૂપમાં કેપેસીટન્સ $C$ કેટલું મળે?
The value of diclectric constant is given as
\(\mathrm{K}=\mathrm{K}_{0}+\lambda \mathrm{x}\)
And, \(\mathrm{V}=\int_{0}^{\mathrm{d}} \mathrm{Edr}\)
\(\mathrm{v}=\int_{0}^{\mathrm{d}} \frac{\sigma}{\mathrm{K}} \mathrm{dx}\)
\({=\sigma \int_{0}^{d} \frac{1}{\left(K_{0}+\lambda x\right.} d x}\)
\({=\frac{\sigma}{\lambda}\left[\ln \left(K_{0}+\lambda d-\ln K_{0}\right]\right.}\)
\({=\frac{\sigma}{\lambda} \ln \left(1+\frac{\lambda d}{K_{0}}\right)}\)
Now it is given that capacitance of vacuum \(=1\)
Thus, \(C=\frac{Q}{V}\)
\(=\frac{\sigma . s}{v}\) (Let surface area of plates \(=\) \(s\))
\(=\frac{\sigma}{\lambda} \ln \left(1+\frac{\lambda \mathrm{d}}{\mathrm{K}_{0}}\right)\)
\( = \operatorname{s} \,\lambda \,\frac{d}{d}\frac{1}{{\ln \left( {1 + \frac{{\lambda d}}{{{K_0}}}} \right)}}\left( {\because {\text{ in vacuum }}{\varepsilon _0} = } \right.\)
\(c=\frac{\lambda d}{\ln \left(1+\frac{\lambda d}{K_{0}}\right)} \cdot C_{0}\left(\text { here, } C_{0}=\frac{s}{d}\right)\)
Download our appand get started for free
Similar Questions
- 1બે સમાન વિદ્યુતભાર $x=-a$ અને $x=+a$ $X$- અક્ષ પર મૂકેલાં છે.વિદ્યુતભાર $Q$ ને ઉદ્ગમ બિંદુ પર મૂકેલ છે.હવે,વિદ્યુતભાર $Q$ ને ઘન $X$- દિશા તરફ સૂક્ષ્મ સ્થાનાંતર $x$ કરાવવામાં આવે,તો તેની વિદ્યુતસ્થિતિઊર્જામાં કેટલો ફેરફાર થાય?View Solution
- 2$X$ અને $Y$ અક્ષ પર શું દર્શાવે છે ( $Y$ પ્રથમ રાશિ છે.)View Solution
- 3બે બિંદુઓ $P$ અને $Q$ આગળ વિદ્યુતસ્થિતિમાનમાં મૂલ્યો અનુક્રમે $10\; V$ અને $-4 \;V$ છે. તો $100$ ઈલેક્ટ્રોનને બિંદુ $P$ થી $Q$ પર લાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 4સમાંતર પ્લેટ કેપેસિટર $C$ ના બે છેડા વચ્ચેનું વિદ્યુતસ્થિતિમાન $V$ હોય, તો આ કેપેસિટરમાં સંગ્રહિત ઊર્જા કેટલી હશે?View Solution
- 5કેપેસિટરનો વોલ્ટેજ $5\ V$ થી $10\ V$ કરવા માટે $W$ કાર્ય કરવું પડે છે,તો વોલ્ટેજ $10\ V$ થી $15\ V$ કરવા માટે કેટલા.......$W$ કાર્ય કરવું પડે?View Solution
- 6દરેક $1$ $\mu$$F$ મૂલ્ય ધરાવતા ત્રણ કેપેસિટરોને એવી રીતે જોડવામાં આવે છે, કે જેથી પરિણામી કેપેસિટન્સ $1.5$ $\mu$$F$ છે, તો....View Solution
- 7$\vec p$ મોમેન્ટ ધરાવતી એક વિદ્યુત ડાઇપોલને વિદ્યુતક્ષેત્ર $\vec E$ ની દિશામાં મૂકેલો છે.આ ડાઇપોલને $90 ^o $ ના કોણે ભ્રમણ કરાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 8$d$ જેટલું પ્લેટોનું અંતર ધરાવતા કેપેસીટરને $V$ સ્થિતિમાટે રાખેલ છે. બેટરીથી છુટો કરી દીધા બાદ તેનામાં $\frac{d}{2}$ જેટલી જાડાઈનો એવો ડાઈઇલેક્ટ્રીક દાખલ કરાય છે કે જેને ડાઈઇલેકટ્ટીક અચળાંક $2$ છે. હવે તેનાં બે છેડાઓ વચ્ચે વિદ્યુત સ્થિતિમાનનો તફાવત કેટલો રહેશે ?View Solution
- 9સમાંતર પ્લેટ કેપેસિટરની બે પ્લેટ વચ્ચેનું અંતર બમણું અને પ્લેટનું ક્ષેત્રફળ અડધું કરવામાં આવે છે. જો $C$ તેનું શરૂઆતનું કેપેસિટન્સ હોય, તો અંતિમ કેપેસિટન્સ કોને બરાબર થાય?View Solution
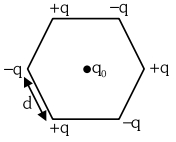
- 10છ વિદ્યુતભાર $+ q ,- q ,+ q ,- q ,+ q$ અને $- q$ ને આકૃતિમાં દર્શાવ્યા મુજબ $d$ બાજુના ષટ્કોણના શિરોબિંદુ પર મૂકેલા છે. અનંતથી ષટ્કોણના કેન્દ્રમાં $q _0$ વિદ્યુતભાર લાવવામાં માટે કેટલું કાર્ય કરવું પડે? $\left(\varepsilon_0-\right.$ મુક્ત અવકાશની પરમિટિવિટી)View Solution