સમક્ષિતિજ પ્લેટફોર્મ શિરોલંબ દિશામાં $ 3.92 \times {10^{ - 3}}\,m $ ના કંપવિસ્તારના દોલનો કરે છે. તેમના પર $m$ દળનો બ્લોક મૂકેલ છે.પ્લેટફોર્મનો આવર્તકાળ કેટલો રાખવો જોઇએ કે જેથી બ્લોક પ્લેટફોર્મ પરથી છુટે નહિ?
AIIMS 1999, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થિર ઉભેલી લીફટની છતથી લટકાવેલા લોલકનો આવર્તકાળ $T_0$ છે. હવે લીફટ જ્યારે અચળ ઝડપથી નીચે તરફ સરકવા લાગે ત્યારે આવર્તકાળ $T_1$ છે અને લીફટ અચળ પ્રવેગથી નીચે તરફ સરક ત્યારે આવર્તકાળ $T_2$ છે. તે સ્થિતિ નીચેનામાંથી ક્યું સાયું હશે ?View Solution
- 2$10$ સેમીનાં કંપવિસ્તાર અને $0.1$ સે. ના આવર્તકાળથી $10$ ગ્રામ દળ ધરાવતો કણ સરળ આવર્તદોલન કરે છે. આ કણ પર લાગતું મહત્તમ બળ (લગભગ) .......... $N$ હશે ?View Solution
- 3સમાન આવર્તકાળ અને $ \pi $ કળા તફાવત ધરાવતી બે એકબીજાને લંબ રહેલ બે સરળ આવર્ત ગતિના સંયોજનના પરિણામથી કણનું સ્થાનાંતર કેવું થાય?View Solution
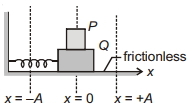
- 4આકૃતિમાં દર્શવ્યા પ્રમાણે બ્લોક $P$ અને $Q$ વચ્ચે ઘર્ષણ છે. પરંતુ $Q$ અને તળિયાની સપાટી વચ્યે ઘર્ષણ લાગતું નથી. સ્પ્રિંગની સામાન્ય સ્થિતિમાં બ્લોક $Q, P$ તે $x=0$ સ્થિતિમાં છે. હવે બ્લોક $Q$ જમણી તરફ થોડો ખેંચીને છોડવામાં આવે છે. આ સ્પ્રિંગ બ્લોક પ્રણાલી $A$ જેટલા કંપવિસ્તારથી દોલનો કરે છે. જો આ સ્થિતિ $P$ બ્લોક $Q$ પરથી સરકવા લાગે તો ક્યા સ્થાને સરકીને નીચે પડશે?View Solution
- 5View Solutionઅવમંદિત દોલનોનો વેગ વિરુદ્ધ સ્થાનનો આલેખ કેવો મળે?
- 6એક સરળ આવર્ત ગતિ કરતાં પદાર્થ માટે આવર્તકાળ $T\, = 0.5\, s$ અને કંપવિસ્તાર $A\,= 1\, cm$ છે. જ્યારે પદાર્થ પોતાના સમતોલન સ્થાન પરથી અડધા કંપવિસ્તાર સુધી ગતિ કરે તે દરમિયાન તેનો સરેરાશ વેગ $cm/s$ માં કેટલો મળે?View Solution
- 7એક સ્પ્રિંગનો આવર્તકાળ $T$ છે અને તેના $n$ સરખા નાના ટૂકડામાં કાપવામાં આવે, તો દરેક ટુકડાનો આવર્તકાળ કેટલો થાય?View Solution
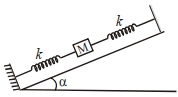
- 8આપેલા આવૃત્તિમાં, $M$ દળ ધરાવતો પદાર્થ બે દળરહિત સ્પ્રિંગો વચ્ચે ઘર્ષણરહિત ઢળતા સમતલ (ઢોળાવ) પર રાખવામાં (બાંધવામાં) આવેલ છે. સ્પ્રિંગોનાં મુક્ત છેડાઓને જડ-આધાર સાથે જોડવામાં આવેલ છે. જે દરેક સ્પ્રિંગનો બળ અચળાંક $k$ હોય તો પદાર્થનાં દોલનની આવૃત્તિ ...... છે.View Solution
- 9સરળ આવર્ત ગતિ કરતા કણ માટે કોઈ ચોક્ક્ચ સમયે સ્થાન, વેગ અને પ્રવેગનાં મૂલ્યો અનુક્મે $4 \mathrm{~m}, 2 \mathrm{~ms}^{-1}$ અને $16 \mathrm{~ms}^{-2}$ છે. આ સમયે ગતિ માટે કંપવિસ્તાર $\sqrt{x} \mathrm{~m}$ છે જ્યાં $x$ ............ હશે.View Solution
- 10$L$ લંબાઇનો તાર છત પર બાંધેલ છે. બીજા છેડા પર $k$ બળઅચળાંક ઘરાવતી સ્પ્રિંગ સાથે બાંધેલ છે. $m$ દળનો પદાર્થ સ્પ્રિંગ સાથે બાંધેલ છે.તારનો આડછેદ $A$ અને યંગમોડયુલસ $Y$ છે. $m$ દળને ખેંચીને મૂકત કરતા સરળ આવર્તગતિનો આવર્તકાળ કેટલો થાય?View Solution