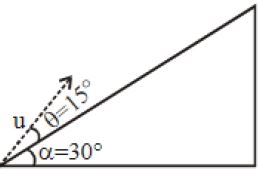
સમક્ષિતિજ સાથે $\alpha = 30^o$ ના ખૂણે રહેલા સમતલ પર એક કણને આકૃતિમાં દર્શાવ્યા મુજબ તળિયેથી $u = 2\,ms^{-1}$ ના વેગથી $\theta = 15^o$ ના ખૂણે પ્રક્ષિપ્ત કરવામાં આવે છે. તો તળિયેથી ........ $cm$ અંતરે કણ સમતલ સાથે અથડાશે?.

JEE MAIN 2019, Diffcult
d
\(\begin{array}{l}
T = \frac{{2\,u\,\sin \theta }}{{g\,\cos \alpha }}\\
R\, = u\,\cos \theta \,T - \frac{1}{2}\,g\,\sin \,\alpha \,{T^2}\\
\,\,\,\,\, = \,\frac{{u\,\cos \,\theta \,2u\,\sin \,\theta }}{{g\,\cos \,\alpha }} - \frac{{g\,\sin \,\alpha }}{2}\frac{{4{u^2}{{\sin }^2}\theta }}{{{g^2}{{\cos }^2}\alpha }}\\
\,\,\,\,\, = \frac{{{u^2}{{\sin }^2}\theta }}{{g\,\cos \,\alpha }} - \frac{{{u^2}\sin \,\alpha }}{{g\,{{\cos }^2}\alpha }}\{ 1 - \cos 2\theta \}
\end{array}\)
\(\begin{array}{l}
T = \frac{{2\,u\,\sin \theta }}{{g\,\cos \alpha }}\\
R\, = u\,\cos \theta \,T - \frac{1}{2}\,g\,\sin \,\alpha \,{T^2}\\
\,\,\,\,\, = \,\frac{{u\,\cos \,\theta \,2u\,\sin \,\theta }}{{g\,\cos \,\alpha }} - \frac{{g\,\sin \,\alpha }}{2}\frac{{4{u^2}{{\sin }^2}\theta }}{{{g^2}{{\cos }^2}\alpha }}\\
\,\,\,\,\, = \frac{{{u^2}{{\sin }^2}\theta }}{{g\,\cos \,\alpha }} - \frac{{{u^2}\sin \,\alpha }}{{g\,{{\cos }^2}\alpha }}\{ 1 - \cos 2\theta \}
\end{array}\)
\(\begin{array}{l}
= \frac{{4 \times \frac{1}{2}}}{{10 \times \frac{{\sqrt 3 }}{2}}} - \frac{{{u^2}\sin \,\alpha }}{{g\,{{\cos }^2}\,\alpha }}\left\{ {1 - \frac{{\sqrt 3 }}{2}} \right\}\\
= \frac{4}{{10\sqrt 3 }} - \frac{8}{{30}}\left\{ {1 - \frac{{\sqrt 3 }}{2}} \right\}\\
= \frac{4}{{5\sqrt 3 }} - \frac{8}{{30}} = \frac{{8\sqrt 3 - 8}}{{30}} = \frac{{8\left( {\sqrt 3 - 1} \right)}}{{30}} = 20\,cm
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો શંકુઆકારનાં લોલકની દોરી સમક્ષિતિજ સાથે $\theta$ કોણ બનાવે છે, તો પછી તેના આવર્તકાળનો વર્ગ કોના સમપ્રમાણમાં હશે?View Solution
- 2કણ ને $u$ વેગથી સમક્ષિતીજ સાથે ખૂણે $\theta$ ફેકવામા આવે તો મહત્તમ ઊચાઇએ તેના વેગમા કેટલો ફેરફાર થાય?View Solution
- 3બે કાગળના પડદાઓ $A$ અને $B$ એ $100 \,m$ જેટલા અંતરે અલગ રાખેલા છે. એક ગોળી $A$ અને $B$ માંથી અનુક્રમે $P$ અને $Q$બિંદુથી પસાર થાય છે, જ્યાં $Q$ એ $P$ થી $10 \,cm$ નીચે છે. જો ગોળી $A$ ને અથડાતા સમયે સમક્ષિતિજ દિશામાં ગતિ કરતી હોય તો $A$ પાસેથી પસાર થવાના સમયે તેનો વેગ ........ $m / s$ હશે.View Solution
- 4એક $u$ વેગથી ગતિ કરતું વિમાન જ્યારે $h$ ઊંચાઈ પર હોય ત્યારે તે એક પેકેટ છોડે છે. તો તેને જમીન પર આવતા લાગતો સમય $t$ કેટલો હશે?View Solution
- 5$0.20m$ ત્રિજયાનું પૈડું સ્થિર સ્થિતિમાંથી $1\;rad/{s^2}$ ના કોણીય પ્રવેગથી ભ્રમણ શરૂ કરે છે. તે ${90^o}$ ખૂણે ફરે, ત્યારે તેના પરિઘ પરના બિંદુનો કેન્દ્રગામી પ્રવેગ કેટલો થશે?View Solution
- 6એક દડાને જમીન પરથી સમક્ષિતિજ સાથે $45^{\circ}$ ના ખૂણે પ્રક્ષેપિત કરવામાં આવે છે. તે ઉગમબિંદુથી $d_1$ અંતરે દૂર રહેલ થાંભલની ટોચ સુધી પહોંચીને જમીન પર થાંભલાથી $d _2$ અંતરે નીચે આવે છે તો થાભલાની ઊંચાઈ શું હશે ?View Solution
- 7View Solutionપ્રક્ષિપ્ત પદાર્થની લઘુત્તમ ગતિઊર્જા કેટલું સમક્ષિતિજ અંતર કાપતાં થાય?
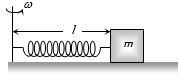
- 8$k$ બળઅચળાંક અને $l$ લંબાઇ ઘરાવતી સ્પ્રિંગના છેડે $m$ દળનો પદાર્થ બાંઘીને સમક્ષિતિજ સમતલમાં $\omega $ કોણીય ઝડપથી ફેરવતા સ્પ્રિંગની લંબાઇમાં કેટલો વધારો થાય?View Solution
- 9નિસરણીની ટોચ પરથી એક દડો સમક્ષિતિજ વેગ $u$ થી ગબડે છે. પગથિયા $0.1$ m ઊંચા અને $0.1 \mathrm{~m}$ પહોળા છે. નિસરણીના $5$ મા પગથિયા પર પડવા માટેનો દડાનો ન્યૂનતમ વેગ $\sqrt{x} m s^{-1}$ હોય છે જ્યા $x=$_________. $\left[\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right.$ લો].View Solution
- 10પ્રક્ષિપ પદાર્થનો મહતમ ઉંચાઈએ વેગ $\frac{\sqrt{3}}{2} u$ હોય અને તેનો શરૂઆતણો વેગ $(u)$ છે. તો સમક્ષિતિજ સમતલમાંમાં તેની અવધી કેટલી હોય ?View Solution
