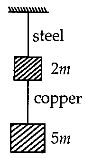
સ્ટીલ અને બ્રાસના તારો માટે લંબાઇઓ,ત્રિજયાઓ અને યંગ મોડયુલસનો ગુણોતર અનુક્રમે $q,p $ અને $s$ હોય,તો તેમને અનુરૂપ લંબાઇમાં વઘવાનો ગુણોતર

Diffcult
b
\(As\,Y = \frac{{FL}}{{A\Delta L}} = \frac{{4FL}}{{\pi {D^2}\Delta L}}\)
\(As\,Y = \frac{{FL}}{{A\Delta L}} = \frac{{4FL}}{{\pi {D^2}\Delta L}}\)
\(\Delta L = \frac{{4FL}}{{\pi {D^2}Y}}\)
\(\therefore \frac{{\Delta {L_s}}}{{\Delta {L_c}}} = \frac{{{F_S}}}{{{F_C}}}\frac{{{L_S}}}{{{L_C}}}\frac{{D_C^2}}{{D_S^2}}\frac{{{Y_C}}}{{{Y_S}}}\)
Where subscripts \('S'\) and \('C'\) refer to copper and steel respectively.
\(Here,\,{F_S} = \left( {5m + 2m} \right)g = 7mg\)
\({F_C} = 5mg\)
\(\frac{{{L_S}}}{{{L_C}}} = q,\frac{{{D_S}}}{{{D_C}}} = p,\frac{{{Y_S}}}{{{Y_C}}} = s\)
\(\therefore \frac{{\Delta {L_S}}}{{\Delta {L_C}}} = \left( {\frac{{7mg}}{{5mg}}} \right)\left( q \right){\left( {\frac{1}{p}} \right)^2}\left( {\frac{1}{s}} \right) = \frac{{7q}}{{5{p^2}s}}\)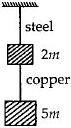
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક તાર (યંગ મોડ્યુલસ $2 \times 10^{11}\, Nm^{-2}$) પર $5 \times 10^7\,Nm^{-2}$ જેટલું પ્રતન પ્રતિબળ લગાવવામાં આવે છે.જો સંપૂર્ણ તારના કદમાં $0.02\%,$ નો ફેરફાર થતો હોય તો તેની ત્રિજ્યા થતો આંશિક ઘટાડો કેટલો હશે?View Solution
- 2$L$ લંબાઈના તારમાં લંબાઈમાં થતો વધારો $l$ છે જો હવે તારની લંબાઈ અડધી કરી દેવામાં આવે તો તેમાં કેટલો વધારો થાય?View Solution
- 3આપેલ ઘન પદાર્થ માટે પોઈસન ગુણોતર $\sigma$ કદ સ્થિતિસ્થાપકતા અંક $(K)$ અને દૃઢતા અંક $(\eta)$ વચ્ચેનો સાચો સંબંધ પસંદ કરો:View Solution
- 4$2 \,m$ લંબાઈ અને $1 \,cm ^2$ આડછેદ ધરાવતા તારનુ તાપમાન $0^{\circ} C$ થી $80^{\circ} C$ સુધી લઈ જવામા આવે છે અને આના લીધે લંબાઈમાં વધારો થતો ન હોય તો જરૂરી બળ કેટલુ લગાવુ જોઈએ? $\left\{Y=10^{10} \,N / m ^2, \alpha=10^{-6} /^{\circ} C \right\}$View Solution
- 5બે સમાન દ્રવ્યમાથી બનાવેલા તારની લંબાઈ અને વ્યાસનો ગુણોત્તર અનુક્રમે $1:2$ અને $2:1$ છે જ્યારે તેને બળ $F_A$ અને $F_B$ વડે ખેચીને લંબાઈમાં સરખો વધારો કરવામાં આવે તો $F_A/F_B$ =_______View Solution
- 6જયારે તાર પર $4N$ નું બળ લગાડવામાં આવે ત્યારે તેની લંબાઇ $a$ છે.જયારે $5N$ નું બળ લગાડવામાં આવે ત્યારે તેની લંબાઇ $b$ છે.તો જયારે $9N$ નું બળ લગાડવામાં આવે ત્યારે તેની લંબાઇ કેટલી થાય?View Solution
- 7$2 \,mm$ વ્યાસ ધરાવતા સ્ટીલના તારનો બ્રેકિંગ ક્ષમતા $4 \times$ $10^5 \,N$ છે. તો સમાન પરીમાણ ધરાવતા $1.5 \,mm$ ના સ્ટીલના તારનો બ્રેકિંગ બળ............ $\times 10^5 \,N$View Solution
- 8$0.1 \,m$ બાજુવાળા સમઘન બ્લોકની ઉપરની બાજુ પર $100 \,N$ નું સ્પર્શીય બળ લગાડતાં તે નીચેની બાજુની સાપેક્ષે $0.02 \,cm$ ખસે છે,તો સ્પર્શીય વિકૃતિ કેટલી થાય?View Solution
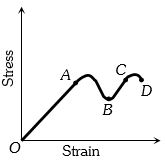
- 9ધાતુ માટે પ્રતિબળ વિરુદ્ધ વિકૃતિનો ગ્રાફ આપેલો છે. ગ્રાફના ક્યાં બિંદુ સુધી હુકના નિયમનું પાલન થાય $?$View Solution
- 10View Solutionએલ્યુમિનિયમ અને કોપર જેવા દ્રવ્યો માટે સ્થિતિસ્થાપક અંકનો સાચો ક્રમ નીચેનામાથી કયો છે?
