સૂર્યને $T\; K$ તાપમાને $R$ ત્રિજ્યાનાં ગોળા તરીકે ધારતાં, સૂર્યમાંથી પૃથ્વી પર આપાત થતો કુલ ઉત્સર્જન પાવર ગણો. પૃથ્વીનું સૂર્યથી અંતર $r$ લો.
જ્યાં $r_{0}$ એ પૃથ્વીની ત્રિજ્યા અને $\sigma$ એ સ્ટીફન અચળાંક છે.
AIEEE 2006, Medium
c
સૂર્ય દ્વારા દરેક સેકન્ડમાં ઉત્સર્જાતી ઉર્જા
સૂર્ય દ્વારા દરેક સેકન્ડમાં ઉત્સર્જાતી ઉર્જા
\(E =\sigma T ^{4} 4 \pi R ^{2}\)
આ ઊર્જા સૂર્યની આસપાસનાં આવરણની આંતરીક સપાટી પર સમાન
રીતે પડે છે. સૂર્ય અને પૃથ્વી વચ્ચેનું અંતર \(r\) હોવાથી \(r\) ત્રિજ્યાનાં ગોળાના એકમ ક્ષેત્રફળ પર દર સેકન્ડે પડતી ઊર્જા
\(\frac{2 \pi R ^{2} \sigma T ^{4}}{2 \pi r ^{2}}=\frac{\sigma R ^{2} T ^{4}}{ r ^{2}}\)
આ ઊર્જા માત્ર સૂર્યનાં સામેના (એક તરફના) અર્ધગોળાકાર ભાગમાંથી
મળતી ઊર્જા છે જે પૃથ્વીનાં માત્ર સામેના અડધા ભાગ પર જ પડે છે.
તેથી \(\frac{4 \pi R^{2}}{2}\) અને \(\frac{4 \pi R^{2}}{2}\) એમ લેવું જોઈએ.
પૃથ્વી પર આપાત થતો ઉત્સર્જન પાવર
\(Q =\pi r _{0}{ }^{2} \times \frac{\sigma R ^{2} T ^{4}}{ r ^{2}}=\frac{\pi r _{0}^{2} R ^{2} \sigma T ^{4}}{ r ^{2}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$727^oC$ તાપમાને રહેલ કાળા પદાર્થનો ઉત્સર્જિત પાવર $60\,\, watt$ અને પરિસરનું તાપમાન $227^oC$ છે. જો કાળા પદાર્થનું તાપમાન બદલીને $1227^oC$ કરવામાં આવે, તો ઉત્સર્જિત પાવર ($watt$ માં) કેટલો થશે?View Solution
- 2એક ઓરડામાં $30 °C$ તાપમાને એક પદાર્થ ઠંડો પાડતા તેનું તાપમાન $75 °C$ થી $ 65 °C$ થતા $2$ મિનિટ લાગે છે તો આ જ ઓરડામાં આજ તાપમાને તેનું તાપમાન $55 °C$ થી $45 °C$ થતા ...... $(\min)$ સમય લાગે ?View Solution
- 3View Solutionએક લોખંડના ટુકડાને જયોતમાં ગરમ કરવામાં આવે છે. પ્રથમ તે ધુંધળો લાલ બને છે, ત્યારબાદ તે રાતાશ પડતો પીળો બને અને છેલ્લે ગરમ સફેદમાં ફેરવાય છે. ઉપરોકત અવલોકનની સાચી સમજૂતી શેના ઉપયોગથી શકય છે.
- 4આકૃતિ $2$ માં ઉષ્માનું વહન $12 sec$ માં થાય, તેટલી જ ઉષ્માનું વહન આકૃતિ $1$ માં થતાં ...... $\sec$ સમય લાગે ?View Solution

- 5સૂર્ય અને ચંદ્રમાંથી આવતા પ્રકાશમાં મહત્તમ તરંગલંબાઇ $ 0.5 \times {10^{ - 6}}m $ અને $ {10^{ - 4}}m $ છે.તો તેમના તાપમાનનો ગુણોત્તર કેટલો થાય ?View Solution
- 6View Solutionવિનના નિયમ અનુસાર....
- 7View Solutionન્યુટનનો શીતનના નિયમ પ્રયોગશાળામાં શું શોધવા માટે ઉપયોગી છે ?
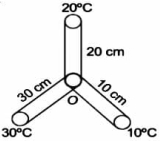
- 8ત્રણ સળીયા સરખા પદાર્થના સરખા ક્ષેત્રફળ ધરાવતા પણ અલગ અલગ લંબાઈ $10 \,cm , 20 \,cm$ અને $30 \,cm$ ધરાવે છે. તો આકૃતિમાં દર્શાવ્યા મુજબ તેના જંકશનનું તાપમાન $O$ ................. $^{\circ} C$ હશે?View Solution
- 9સમાન લંબાઇ અને સમાન વ્યાસ ધરાવતા બે સળિયા $P$ અને $Q$ ની ઉષ્માવાહકતાનો ગુણોત્તર $2:3$ છે.બંનેને જોડવામાં આવે છે. $P$ ના છેડાને $100^°C$ અને $Q$ ના છેડાને $0^°C$ રાખવામાં આવે છે,તો સંપર્ક સપાટીનું તાપમાન...... $^oC$View Solution
- 10એક પદાર્થ $5$ મિનિટમાં $80^{\circ}\,C$ માથી $60^{\circ}\,C$ સુધી ઠંડો પડે છે.પરિસરનું તાપમાન $20^{\circ}\,C$ છે.તો તેને $60^{\circ}\,C$ થી $40^{\circ}\,C$ સુધી ઠંડો પડવા માટેનો સમય .......... $s$ થશે.View Solution
