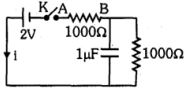
આકૃતિ \((i)\)
\(t = 0\) સમયે \(C\) માથી થી પ્રવાહ વધે છે અને તેનો \(R_C = 0\)
\(I\, = \,\,\frac{2}{{1000}}\,\, = \,\,2\ mA\)
\( t = \infty \) સમયે, અથવા થોડા સમય પછી \(C\) માંથી વિુતપ્રવાહ વહેતો નથી તેનો \(R_C = \infty \)
આકૃતિ \((ii)\)
\(i\, = \,\,\frac{V}{{{R_{total}}}}\,\, = \,\,\,\frac{2}{{2000}}\,\, = \,\,1\ mA\)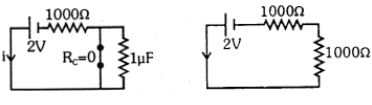
Download our appand get started for free
Similar Questions
- 1નીચે બે વિધાનો આપેલાં છે. એકને કથન $A$ અને બીજાને કારણા $R$ વડે દર્શાવેલ છે.View Solution
કथન $A: 4 \times 10^{-6} \mathrm{C}$ $m$ના મૂલ્યની દ્રી-ધ્રુવી ચાકમાત્રા $\vec{P}$. ધરાવતી દ્રી-ધ્રુવીના કેન્દ્રથી $2 \mathrm{~m}$ અંતરે $(r)$ રહેલ કોઈ અક્ષીય બિંદુ આગળ સ્થિતિમાન $(\mathrm{V}) \pm 9 \times 10^3 \mathrm{~V}$ છે.
$\left[\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \text { SI એકમ }\right]$
કારણ $R: V= \pm \frac{2 P}{4 \pi \epsilon_0 r^2}$, જ્યાં $r$ એ કોઈ અક્ષીય બિંદુનું
ત્રિજ્યાવર્તી દિશામાં અંતર છે કે જે દ્વિ-ધ્રુવીનાં કેન્દ્રથી $2 \mathrm{~m}$ અંતરે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિક્લ્પોમાંથી સાચો ઉત્તર ૫સંદ કરો.
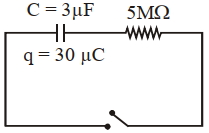
- 2$3\, \mu F$ કેપેસિટર પર $30\, \mu C$ વિધુતભાર છે,$t =0$ સમયે કળ બંધ કરતાં $5\, M \Omega$માંથી પસાર થતો પ્રવાહ $'x'$ $\mu-A$ હોય તો $'x' \,=.........$View Solution
- 3$5\, km$ પહોળાઈ અને $5\, km$ લંબાઈ ધરાવતો એક વિશાળ જળવાદળ છે. તેનું તળિયું (પાયો અહી દર્શાવ્યા પ્રમાણે પૃથ્વીની સપાટીથી $1\, km$ ઉપર છે. ડાઈ ઈલેકટ્રીક તરીકે હવાના માધ્યમ સાથે પૃથ્વીની સપાટી અને વાદળને સમાંતર પ્લેટ કેપેસિટર હોય તેમ ધારો તો વાદળ અને પૃથ્વી સપાટી સંયોજનનું કેપેસિટન્સ........$\mu F$ માં શોધો.View Solution

- 4વિદ્યુતભારિત ગોળીય બોલ માટે, બોલની અંદર સ્થિત વિદ્યુત સ્થિતિમાન, ત્રિજ્યા સાથે $V=2 a r^2+b$ પ્રમાણે બદલાય છે. અત્રે, $a$ અને $b$ અચળાંકો છે અને $r$ એ કેન્દ્રથી અંતર છે. બોલની અંદર વિદ્યુતભાર ધનતા $-\lambda a \varepsilon$ છે. $\lambda$ નું મૂલ્ય $..............$ થશે.View Solution
- 5નીચેના પરિપથમાં દર્શાવેલા સંઘારકના તંત્રની સમતુલ્ય સંઘારકતા $...........\mu F$ છે.View Solution
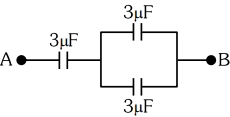
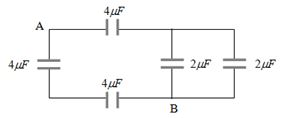
- 6આકૃતીમાં દર્શાવ્યા મુજબ $A$ અને $ B$ વચ્ચેનુંં સમતુલ્ય કેપેસીટન્સ....$\mu F$View Solution
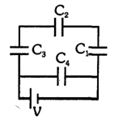
- 7$C_1 =1\ C, C_2 = 2\ C, C_3 = 3 \ C$ અને $C_4 = 4\ C$ ને સમાન કેપેસિટન્સ ધરાવતા ચાર કેપેસિટરોના નેટવર્કને આકૃતિ મુજબ, બેટરી સાથે જોડવામાં આવે છે. તો $C_2$ અને $C_4$ પરના વિદ્યુત ભારોનો ગુણોત્તર શોધો.View Solution
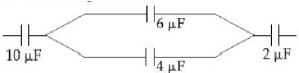
- 8નીચે દર્શાવેલ આકૃતિમાં $10 \,\mu F$ ના કેપેસિટરની ડાબી બાજુની પ્લેટ પર $-30\, \mu F$ વિજભાર છે. $6\, \mu F$ ના કેપેસિટરની જમણી બાજુની પ્લેટ પર નો વિજભાર.....$\mu C$View Solution
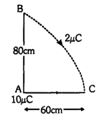
- 9આકૃતિમાં કિરણ વડે દર્શાવેલ પથ પરથી $2\ \mu C$ નો વિદ્યુતભાર $B$ થી $C$ બિંદુએ પહોચે છે. તો થતું કાર્ય ........$J$ ગણો.View Solution
- 10View Solutionએક કેપેસિટરનું કેપેસિટન્સ ..... પર આધારિત છે.
