ત્રણ સમાન દ્રવ્ય, સમાન લંબાઈ અને સમાન આડછેદ વાળા સળિયાને જોડીને આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલા છે.ડાબી અને જમણી બાજુને અનુક્રમે ${0^o}C$ અને ${90^o}C$ તાપમાને રાખેલ છે. તો ત્રણેય સલિયાના જંકશન પાસેનું તાપમાન ....... $^oC$ થાય?
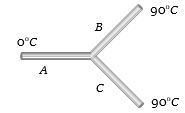

IIT 2001, Medium
b
(b) Let the temperature of junction be \(\theta\). Since roads \(B\) and \(C\) are parallel to each other (because both having the same temperature difference).
(b) Let the temperature of junction be \(\theta\). Since roads \(B\) and \(C\) are parallel to each other (because both having the same temperature difference).
Hence given figure can be redrawn as follows
( \(\frac{Q}{t} = \frac{{({\theta _1} - {\theta _2})}}{R}\) and \({\left( {\frac{Q}{t}} \right)_{AB}} = {\left( {\frac{Q}{t}} \right)_{BC}}\)
==> \(\frac{{(90 - \theta )}}{{R/2}} = \frac{{(\theta - 0)}}{R}\)
==> \(180 - 2\theta = \theta \)
==>\(\theta = 60^\circ C\)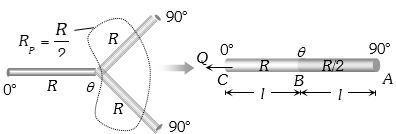
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionવિધાન : બે પાતળા ભેગા કરેલા ધાબળા એ એક બમણી જાડાઈ ધરાવતા એક ધાબળા કરતાં વધુ ગરમ લાગે
કારણ : બે પાતળા ધાબળા વચ્ચેનું હવાનું પડને લીધે જાડાઈ વધે છે.
- 2View Solutionઉષ્માનો સારો શોષક એ ઉષ્માનો
- 3કલ્પના કરો કે સૂર્યની બહારની ગોળાકાર સપાટીની ત્રિજયા $r$ છે અને તે $t^oC$ જેટલા તાપમાને સંપૂર્ણ કાળા પદાર્થની માફક ઊર્જાનું ઉત્સર્જન કરે છે, તો સૂર્યના કેન્દ્રથી $R$ જેટલા અંતરે આવેલ એકમ ક્ષેત્રફળવાળી સપાટી (જે આપાતકિરણોને લંબરૂપે છે. ) વડે મેળવાતો પાવર કેટલો હશે?View Solution
જ્યાં $\sigma=$ સ્ટિફનનો અચળાંક છે.
- 4View Solutionવિનના નિયમ અનુસાર....
- 5ત્રણ સળીયા સરખા પદાર્થના સરખા ક્ષેત્રફળ ધરાવતા પણ અલગ અલગ લંબાઈ $10 \,cm , 20 \,cm$ અને $30 \,cm$ ધરાવે છે. તો આકૃતિમાં દર્શાવ્યા મુજબ તેના જંકશનનું તાપમાન $O$ ................. $^{\circ} C$ હશે?View Solution
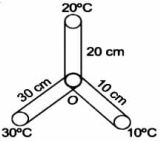
- 6View Solutionઉષ્માકિરણોનો અવકાશમાં વેગ
- 7$3.1 m$ લંબાઇ ધરાવતા સળિયાના એક છેડાને $100^°C$ તાપમાનવાળા પાણીમાં અને બીજા છેડા $ {0^o}C $ તાપમાનવાળા બરફમાં રાખવામાં આવે છે. $200^°C$ તાપમાનવાળી જયોતને કેટલા અંતરે મૂકવાથી બરફનું પાણી અને પાણીની વરાળ સમાન દરથી થાય?બરફની ગલનગુપ્ત ઉષ્મા $80 cal/gm$ અને પાણીની બાષ્પાયનગુપ્ત ઉષ્મા $540 cal/gm$ છે.View Solution

- 8બે પદાર્થ $A$ અને $B$ જેનું વજન, ક્ષેત્રફળ અને બાહ્ય સપાટી એક સરખાં છે જેની વિશિષ્ટ ઉષ્મા $S_A$ અને $S_B\left(S_A > S_B\right)$ છે તેમને આપેલા તાપમાને ઠંડા પાડવામાં આવે છે તો સમય સાથે તાપમાનમાં કેટલો ફેરફાર થાય?View Solution
- 9View Solutionનીચેનામાંથી કયું આદર્શ સંપૂર્ણ કાળા પદાર્થની નજીકનું છે?
- 10View Solutionશિયાળામાં સવારે ધાતુની સપાટી લાકડાની સપાટી કરતાં વધુ ઠંડી લાગે કારણ કે...
