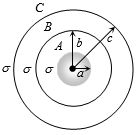
\({\sigma _A} = \sigma = \frac{{{q_a}}}{{4\pi {a^2}}}\,\,\, \Rightarrow \,\,{q_a} = \sigma \times 4\pi {a^2}\),
\({\sigma _B} = - \sigma = \frac{{{q_b}}}{{4\pi {b^2}}}\,\, \Rightarrow \,\,{q_b} = - \sigma \times 4\pi {b^2}\)
\({\sigma _C} = \sigma = \frac{{{q_c}}}{{4\pi {c^2}}}\, \Rightarrow \,{q_c} = \sigma \times 4\pi {c^2}\)
\({V_A} = {({V_A})_{{\rm{surface}}}} + {({V_B})_{{\rm{in}}}} + {({V_C})_{{\rm{in}}}}\)\( = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{{q_a}}}{a} + \frac{{{q_b}}}{b} + \frac{{{q_c}}}{c}} \right]\)
\( = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{\sigma \times 4\pi {a^2}}}{a} + \frac{{( - \sigma ) \times 4\pi {b^2}}}{b} + \frac{{\sigma \times 4\pi {c^2}}}{c}} \right]\)\({V_A} = \frac{\sigma }{{{\varepsilon _0}}}\left[ {a - b +c]} \right]\)
\({V_B} = {({V_A})_{{\rm{out}}}} + {({V_B})_{{\rm{surface}}}} + {({V_C})_{{\rm{in}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{{q_a}}}{b} + \frac{{{q_b}}}{b} + \frac{{{q_c}}}{c}} \right]\)
\( = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{\sigma \times 4\pi {a^2}}}{b} - \frac{{\sigma \times 4\pi {b^2}}}{b} + \frac{{\sigma \times 4\pi {c^2}}}{c}} \right]\)\( = \frac{\sigma }{{{\varepsilon _0}}}\left[ {\frac{{{a^2}}}{b} - b + c} \right]\)
Download our appand get started for free
Similar Questions
- 1આપેલ વિધુતભાર માટે $A$ પર વોલ્ટેજ કેટલો થાય?View Solution
- 2બેટરીથી દૂર કરેલ એક કેપેસિટરનો કેપેસિટન્સ $C_o$ અને ઊર્જા $W_o$ અને છે.હવે ડાઇઇલેકિટ્રક અચલાંક $=$ $5$ ભરી દેતા નવોં કેપેસિટરનો કેપેસિટન્સ અને ઊર્જા કેટલી થાય?View Solution
- 3સમાંતર પ્લેટ કન્ડેન્સરની બે પ્લેટ વચ્ચેનું અંતર $8 \,cm$ હોય ત્યારે તેની કેપેસિટી $10\,\mu \,F$ છે. હવે જ્યારે બે પ્લેટ વચ્ચેનું અંતર ઘટાડીને $4\, cm$ કરવામાં આવે ત્યારે તેની કેપેસિટી કેટલા $\mu \,F$ ની થાય?View Solution
- 4$C$ કેપેસીટન્સ ધરાવતા કેપેસીટરને $V$ વોલ્ટની બેટરી સાથે સમાંતરમાં જોડવામાં આવેલ છે હવે વિદ્યુતભાર સમાન રાખીને કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર અડધું કરવામાં આવે છે તથા ફરીથી તેને $V$ વોલ્ટ સુધી વિદ્યુતભારીત કરવામાં આવે તો બેટરી દ્વારા અપાતી ઉર્જા...?View Solution
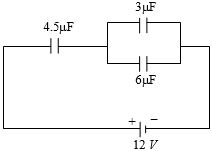
- 5આપેલ તંત્રમાં $4.5\ \mu\ F$ વચ્ચે વિધુતસ્થિતિમાનનો તફાવત કેટલા .....$V$ થાય?View Solution
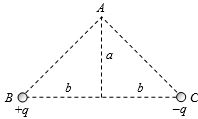
- 6એક સૂક્ષ્મ વિદ્યુત ડાઈપોલની દ્વિ ધ્રુવીય ચાકમાત્રા $p$ એ છે. તેના કેન્દ્રથી '$r$' અંતરે અને ડાઈપોલની અક્ષ સાથે છે. ખૂણો બનાવતા બિંદુ આગળ વિદ્યુત સ્થિતિમાન ....... હશે.View Solution
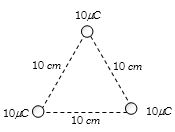
- 7આપેલ તંત્રની કુલ વિદ્યુતસ્થિતિઊર્જા કેટલા .......$J$ થાય? ( $\frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\ N - {m^2}/{C^2})$View Solution
- 8સમાંતર પ્લેટ કેપેસિટરની પ્લેટોનું ક્ષેત્રફળ $A$ છે. અને પ્લેટો વચ્ચેનું અંતર $100\, mm$ છે. તેમાં બે ડાઈ ઈલેકટ્રીક સ્તરો છે. એક $10$ ડાઈ ઈલેકટ્રીક અચળાંક અને $6\, mm$ જાડાઈ ધરાવતું અને બીજુ $5$ ડાઈ ઈલેકટ્રીક અચળાંક અને $4\, mm$ જાડાઈ ધરાવતું છે. તો કેપેસિટરની કેપેસિટન્સ શોધો.View Solution
- 9View Solutionજો નક્કર અને પોલા સુવાહક ગોળાની ત્રિજ્યા સમાન હોય તો,
- 10$10^{-6} \mu \mathrm{C}$ નો એક વીજભાર $X-Y$ યામ પધ્ધતિના ઉગમબિંદુ $(0,0) \mathrm{m}$ પર મૂકેલો છે. બિંદુઓ $\mathrm{P}$ અને $\mathrm{Q}$ અનુક્રમે $(\sqrt{3}, \sqrt{3}) \mathrm{m}$ અને $(\sqrt{6}, 0) \mathrm{m}$ પર રહેલા છે. બિંદુઓ$\mathrm{P}$ અને $\mathrm{Q}$ વચચેનો સ્થિતિમાન તફાવત_____થશે.View Solution
