વિદ્યુતક્ષેત્ર શોધવા ગાઉસનો નિયમ $|\overrightarrow{\mathrm{E}}|=\frac{q_{\mathrm{enc}}}{\varepsilon_{0}|\mathrm{A}|}$ વાપરવામાં આવે છે.જ્યાં $\varepsilon_{0}$ શૂન્યાવકાશની પરમિટિવિટી, $A$ ગાઉસીયન સપાટીનું ક્ષેત્રફળ અને $q_{enc}$ એ ગાઉસીયન સપાટીની અંદર રહેલ વિજભાર છે.ઉપરનું સૂત્ર ક્યારે વાપરવામાં આવે છે?
JEE MAIN 2020, Medium
Download our app for free and get started
d
\(|\overrightarrow{\mathrm{E}}|\) should be constant on the surface and the surface should be equipotential.
\(|\overrightarrow{\mathrm{E}}|\) should be constant on the surface and the surface should be equipotential.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકૃતિમાં દર્શાવ્યા અનુસાર ત્રણ અનંત લંબાઈ ધરાવતી વિદ્યુતભારીત પાતળી શીટ (તકિત)ને ગોઠવવામાં આવે છે. $P$ બિંદુ આગળ વિદ્યુત ક્ષેત્રનું મૂલ્ય $\frac{x \sigma}{\epsilon_o}$ મળે છે. $x$ નું મૂલ્ય. . . . . .હશે. (દરેક રાશિ $SI$ એકમ પદ્ધતિમાં માપવામાં આવેલ છે.)View Solution
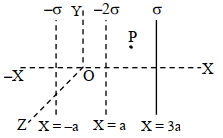
- 2જો ડાઇપોલની અક્ષ પર $x$ જેટલા અંતરે વિદ્યુતક્ષેત્રની તિવ્રતા તેની વિષૃવરેખા પર $y$ જેટલા અંતરે વિદ્યુતક્ષેત્રની તિવ્રતા સમાન હોય તો $x:y$ ....View Solution
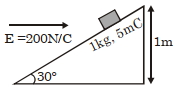
- 3આકૃતિમાં દર્શાવ્યા મુજબ $200 \, \frac{ N }{ C }$ સમાન સમક્ષિતીજ વિદ્યુત ક્ષેત્રમાં મૂકેલ ઢળતી સપાટી, સમક્ષિતીજ સાથે $30^{\circ}$ નો કોણ રચે છે. $1\, kg$ દળ અને $5\, mC$ વિજભાર ધરાવતા પદાર્થને આ ઢળતી સપાટી $1\, m$ ઊંચાઈ વિરામ સ્થાનેથી સરકવા દેવામાં આવે છે. જો ઘર્ષણાંક $0.2$ હોય તો તળીયે પહોંચવા માટે લીધેલો સમય શોધો.($s$ માં)View Solution
$\left[ g =9.8 \,m / s ^{2}, \sin 30^{\circ}=\frac{1}{2}\right.$; $\left.\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$
- 4જો $a$ બાજુવાળા સમઘનના કોઇ એક ખૂણા પર બિંદુવત વિદ્યુતભાર $Q$ છે, તો આ સમઘનમાંથી પસાર થતું કુલ ફલક્સ કેટલું હશે?View Solution
- 5View Solutionબિંદુવત વિદ્યુતભારને લીધે ઉદભવતા વિદ્યુતક્ષેત્રમાં વિદ્યુત ડાઈપોલ મૂકેલ છે.
- 6$d$ વિજભારિત ગોળા વચ્ચે લાગતું બળ $F$ છે. તેને ડાઈઇલેક્ટ્રિક અચળાંક $2$ ધરાવતા પ્રવાહીમાં તેટલા અંતરે મૂકવાથી નવું બળ કેટલું થાય?View Solution
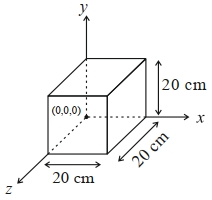
- 7વિદ્યુતક્ષેત્રને $\vec{E}=4000 x^2 \hat{i} \frac{ V }{ M }$ સમીકરણ વડે રજૂ કરેલ છે. $20\,cm$ ની બાજુ (આકૃત્તિમાં દર્શાવ્યા અનુસાર) ધરાવતા સમધનમાંથી પસાર થતું ફ્લક્સ $................V\,cm$ થશે.View Solution
- 8ગોળા અંદર વિદ્યુતભાર $+ 2 × 10^{-6}\ C, -5 × 10^{-6}\ C, -3 × 10^{-6}\ C, +6 × 10^{-6}\ C$ હોય,તો ગોળામાંથી કેટલું ફલ્કસ પસાર થાય?View Solution
- 9View Solutionશૂન્યાવકાશમાં કોઈ બિંદુએ વિદ્યુતક્ષેત્રની તીવ્રતા
- 10$R$ ત્રિજ્યા ધરાવતા એક ગોલીય કવચ પર નિયમિત પૃષ્ઠ વીજભાર ઘનતા $\sigma$ છે. ગોલીય કવચની સપાટી ઉપર કોઈ પણ બિંદુ આગળ વિદ્યુતક્ષેત્ર. . . . . થશે.View Solution