વિદ્યુતસ્થિતિમાન $V = 6x - 8x{y^2} - 8y + 6yz - 4{z^2}$ હોય,તો ઉદ્ગમ બિંદુ પર મૂકેલાં $2\,C$ વિદ્યુતભાર પર કેટલા ......$N$ બળ લાગે?
Medium
Download our app for free and get started
d
(d) \({E_x} = - \frac{{dV}}{{dx}} = - (6 - 8{y^2}),\)\({E_y} = - \frac{{dV}}{{dy}} = - ( - \,16xy - 8 + 6z)\)
\({E_z} = - \frac{{dV}}{{dz}} = - \,(6y - 8z)\)
At origin \(x = y = z = 0\) so,\({E_x} = - \,6,\,{E_y} = 8\) and \({E_z} = 0\)
\(==>\) \(E = \sqrt {E_x^2 + E_y^2} = 10\,N/C\).
Hence force \(F = QE = 2 \times 10 = 20\,N\)
(d) \({E_x} = - \frac{{dV}}{{dx}} = - (6 - 8{y^2}),\)\({E_y} = - \frac{{dV}}{{dy}} = - ( - \,16xy - 8 + 6z)\)
\({E_z} = - \frac{{dV}}{{dz}} = - \,(6y - 8z)\)
At origin \(x = y = z = 0\) so,\({E_x} = - \,6,\,{E_y} = 8\) and \({E_z} = 0\)
\(==>\) \(E = \sqrt {E_x^2 + E_y^2} = 10\,N/C\).
Hence force \(F = QE = 2 \times 10 = 20\,N\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાંતર પ્લેટ કેપેસિટર $C$ ના બે છેડા વચ્ચેનું વિદ્યુતસ્થિતિમાન $V$ હોય, તો આ કેપેસિટરમાં સંગ્રહિત ઊર્જા કેટલી હશે?View Solution
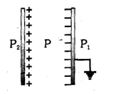
- 2સમાંતર પ્લેટો કેપિસિટરની બે ધાતુની પ્લેટો છે. એક પ્લેટને $+q$ વિદ્યુતભાર આપેલો છે. જ્યારે બીજાને જમીન સાથે જોડેલ છે. સંલગ્ન આકૃતિમાં દર્શાવ્યા પ્રમાણે $P, P_1$ અને $P_2$ બિંદુઓ લીધેલા છે. તો કયા બિંદુએ વિદ્યુત ક્ષેત્ર શૂન્ય નથી ?View Solution
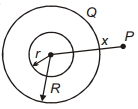
- 3ત્રિજ્યા $r$ અને $R$ ના બે કેન્દ્રિત પોલા વાહક ગોળાઓ બતાવવામાં આવ્યા છે. બાહ્ય શેલ પરનો ચાર્જ $Q$ છે. આંતરિક ગોળાને કયો ચાર્જ આપવો જોઈએ જેથી બાહ્ય ગોળાની બહાર કોઈપણ બિંદુએ $P$ સંભવિત પોટેન્શિયલ શૂન્ય હોય?View Solution
- 4$q$ અને $-q$ વિદ્યુતભાર ધરાવતાં બે સરખાં વાહક ગોળાઓ એકબીજાથી $d$ જેટલાં અંતરે હવામાં રહેલા છે. બંને ગોળાઓની ત્રિજ્યા $r$ છે અને બંને ગોળાઓ વચ્ચેનું અંતર બંને ગોળાઓથી બનતી પ્રણાલીનું કેપેસીટન્સ મેળવો.View Solution
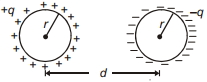
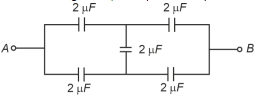
- 5આપેલ પરિપથમાં, છેડા $A$ અને છેડા $B$ વચ્ચે સમતુલ્ય સંધારકતાView Solution
. . . . . . .છે
- 6જ્યારે પ્રોટોનને $1\,V$ ના વિદ્યુતસ્થિતિમાન વડે પ્રવેગિત કરવામાં આવે તો.તેની ગતિઉર્જા કેટલા $eV$ થાય?View Solution
- 7નીચે આપેલામાંથી કયો વક્ર $(R)$ ત્રિજ્યાના વિદ્યુતભારીત ગોળાના સ્થિતિમાન $(V)$ નો, કેન્દ્રથી ત્રિજ્યાવર્તી દિશામાં અંતર $(r)$ સાથેનો ફેરફાર સાચી રીતે રજૂ કરે છે ?View Solution
- 8View Solutionપુરો વિદ્યુતભાર થયેલા એક સમાંતર પ્લેટવાળા કેેેસીટરને બેટરી સાથે જોડેલ રાખીને અવાહક સાધનો વડે તેની પ્લેટોને એકબીજાથી દૂર કરવામાં આવે છે. આ સ્થિતિમાં નીચેનામાંથી કઈ રાશિનું મૂલ્ય ઘટશે?
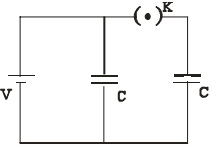
- 9દર્શાવ્યા અનુસાર $V$ જેટલો સ્થિતિમાનનો તફાવત ધરાવતા ઉદગમને બે એક સમાન સંધારકો સાથે જોડવામાં આવેલ છે. જ્યારે કળ ' $K$ ' બંધ હોય છે, ત્યારે આ સંયોજન સમાંતર સંગ્રહિત કુલ ઊર્જા $E_1$ છે. હવે કળ ' $K$ ' ને ખોલવામાં આવે છે અને $5$ જેટલો ડાયઈલેકટ્રીક અચળાંક ધરાવતા ડાયઈલેકટ્રીક માધ્યમને સંધારકોની પ્લેટો વચ્ચે દાખલ કરવામાં આવે છે. આ સંયોજનને સમાંતર સંગ્રહ પામતી કુલ ઊર્જા હવે $E_2$ થાય છે. ગુણોત્તર $E_1 / E_2 \ldots$ થશે.View Solution
- 10$10^{3 }\ m$ વ્યાસ ધરાવતો ધાતુ ગોળાના સ્વરૂપમાં એક રેડિયો એકટિવ પદાર્થ પ્રતિ સેકન્ડે $6.25 \times 10^{10}$ કણોના અચળ દરે કણોનું ઉત્સર્જન કરે છે. જો વાહક વિદ્યુતીય રીતે અલગ કરેલો હોય, તો તેનો સ્થિતિમાન $1.0$ વોલ્ટ, વધારવા માટે કેટલો સમય લેશે? $80\%$ ઉત્સર્જિત કણો સપાટી પરથી બહાર નીકળે છે. તેમ ધારો.......$\mu s$View Solution