$X- $ અક્ષની દિશામાં ગતિ કરવા માટે મુકત એવા $1\; kg $ દળના પદાર્થ માટે સ્થિતિ-ઊર્જા નીચેના સૂત્રથી મળે છે: $U\left( x \right) = \left( {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right)$ $J $ તેની યાંત્રિક ઊર્જા $2\;J $ છે,તો તેની મહત્તમ ઝડપ $m/s$ માં કેટલી થાય?
AIEEE 2006, Medium
a
\(K \cdot E _{\max }= E _{ t }- U _{\min }\)
\(K \cdot E _{\max }= E _{ t }- U _{\min }\)
અહી, \(U( x )=\frac{ x ^{4}}{4}-\frac{ x ^{2}}{2}\)
\(\therefore \frac{ dV }{ dx }=\frac{4 x ^{3}}{4}-\frac{2 x }{2}= x ^{3}- x\)
જ્યારે \(U\) લઘુતમ થાય ત્યારે \(\frac{ dV }{ dx }=0\)
\(\therefore x ^{3}- x =0\)
\(\therefore x \left( x ^{2}-1\right)=0\)
\(\therefore x =0, \pm 1\)
\(U_{\min }(x=\pm 1)=\frac{1}{4}-\frac{1}{2}=-\frac{1}{4} J\)
\(K . E_{\max }=2-\left(-\frac{1}{4}\right)=\frac{9}{4} J =\frac{1}{2} mv _{\max }^{2}\)
\(\therefore v _{\max }^{2}=\frac{2 \times 9}{4}=\frac{9}{2}\)
\(\therefore v _{\max }=\frac{3}{\sqrt{2}} m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,s$ માં $100 \,m$ ઊંચાઈ સુધી $500 \,kg$ પાણીને પંપ કરી શકે એવા પંપનો પાવર ........... $kW$ છે...View Solution
- 2View Solutionકણોના એેક તંત્ર અંદરની અંદર લાગતા આંતરિક બળો કોને બદલી શકે
- 3View Solutionએક ચલ બળની અસર હેઠળ ગતિ કરી રહેલ એક કણ માટેનો ગતિઊર્જા - સ્થિતિ(સ્થાન)નો ગ્રાફ આપેલ છે, તો...
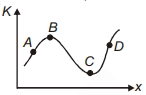
- 4View Solutionઘર્ષણ બળ દ્વારા થયેલું કાર્ય
- 5$100 N/m$ બળ અચળાંક વાળી એક સ્પ્રિંગ $5 cm$ સુધી ખેંચાયેલી છે તો થતું કાર્ય શોધો.View Solution
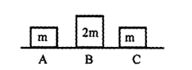
- 6ત્રણ પદાર્થ $A, B, C$ ને ઘર્ષણ રહિત સમક્ષિતિજ સપાટી પર રાખેલા છે તેમના દળો અનુક્રમે $m, 2m $ અને $m$ છે. પદાર્થ $A, B$ ની દિશામાં $9 m/s$ ની ઝડપે ગતિ કરે છે અને તેની સાથે સ્થિતિ સ્થાપક સંઘાત કરે છે. ત્યાર પછી $B,C$ સાથે સંપૂર્ણ અસ્થિતિ સ્થાપક સંઘાત કરે છે. બધી જ ગતિ સમાન સુરેખ રેખા પર થાય છે. પદાર્થ $C$ ની અંતિમ ઝડપ $m/s$ માં કેટલા ................ $\mathrm{m} / \mathrm{s}$ હશે ?View Solution
- 7$1\, m$ લંબાઇ અને ${60^o}$ ખૂણાવાળા ઢાળ પર $1\, kg$ નો બ્લોક મૂકતાં ઘર્ષણ વિરુધ્ધ ...... $J$ કાર્ય થશે. (ગતિક ઘર્ષણાંક $0.5$ છે)View Solution
- 8એક પવન સંચાલિત જનરેટર પવન ઉર્જા ને વિદ્યુતઉર્જામાં રુપાંતરીત કરે છે.ધારો કે જનરેટર તેના પાંખિયા દ્વારા પવનઉર્જાના ઘર્ષણ ને વિદ્યુત ઉર્જા માં રુપાંતરીત કરે છે.પવનની ઝડપ $v$ માટે, મેળવેલ વિદ્યુત પાવર કઈ રીતે સમપ્રમાણ માં હશે?View Solution
- 9બળ ક્ષેત્રમાં કણની સ્થિતિ ઊર્જા $U=\frac{A}{r^{2}}-\frac{B}{r}$ દ્વારા આપવામાં આવે છે, જ્યાં $A$ અને $B$ ધન અચળાંકો છે અને $r$ એ ક્ષેત્રના કેન્દ્રથી કણનું અંતર છે. સ્થાયી સંતુલન માટે કણનું અંતર કેટલું હોવું જોઈએ?View Solution
- 10જો બે અણું વચ્ચેની સ્થિતિઉર્જાને $U =\frac{-A }{ r ^{6}}+\frac{ B }{ r ^{12}},$ વડે આપવામાં આવે તો સંતુલન સમયે બે અણું વચ્ચેનું અંતર અને સ્થિતિઉર્જા કેટલી હશે?View Solution
