(B) $ x$ ધારો કે, કણના વેગમાનની અચોક્કસતા=$\Delta P_{(x)}$
$y$ કણની વેગમાનની અચોક્કસતા=$\Delta P_{(y)}$
$x$ કણના સ્થાનની અચોક્કસતા =$\Delta X_{(x)}$
$y$ કણના સ્થાનની અચોક્કસતા =$\Delta X_{(y)}$
હવે $\Delta {P_{(x)}}\,\, = \,\,\frac{{\Delta {P_{(y)}}}}{2}\,\,\,\Delta {x_{(x)}}\, \times \,\Delta {P_{(x)}}\,\, = \,\,\frac{h}{{4\pi }}\,\,\,\therefore \,\,\Delta {x_{(x)}}\, \times \,\frac{{\Delta {P_{(y)}}}}{2}\, = \,\frac{h}{{4\pi }}$
$\therefore \,\,0.05\, \times \,\Delta {P_{(y)}}\,\, = \,\,\frac{{2h}}{{4\pi }}\,\,\,\therefore \,\,\Delta {P_{(y)}}\,\, = \,\,\frac{{2h}}{{4\pi \, \times \,0.05}}\,\,\Delta {x_{(y)}}\, \times \,\Delta {P_{(y)}}\,\, = \,\,\frac{h}{{4\pi }}$
$\therefore \,\Delta {x_{(y)}}\, \times \,\frac{{2h}}{{4\pi \, \times \,0.05}}\,\, = \,\,\frac{h}{{4\pi }}\,\,\,\therefore \,\,\Delta {x_{(y)}}\,\, = \,\,\frac{{h\, \times \,4\pi \, \times \,0.05}}{{4\pi \, \times \,2h}}\,\,\,\therefore \,\,\Delta {x_{(y)}}\,\, = \,\,0.025\,\mathop A\limits^ \circ $
$\Delta {x_{(y)}} \,=\, $ $2.5 \times 10^{-10}$ સેમી
Download our appand get started for free
Similar Questions
- 1જ્યારે એક ઈલેક્ટ્રોન પાંચમી ઉત્તેજિત અવસ્થામાંથી પ્રથમ ઉત્તેજિત અવસ્થામાં સંક્રાંતિ કરે છે ત્યારે $\mathrm{He}^{+}$વર્ણપટમાં પ્રાપ્ત થતી વાર્ણપટ રેખાઓની સંખ્યા શું થશે?View Solution
- 2View Solutionનીચે આપેલી સંક્રાતિની શ્રેણીઓમાંથી કઇ હાઇડ્રોજન પરમાણુના દ્રશ્યમાન વર્ણપટ વિસ્તારમાં પડે છે ?
- 3View Solutionનીચેના માંથી સાયક્લોટ્રોન કોને પ્રવેગિત કરી શકતું નથી ?
- 4$C{O_2}$ ના એક અણુ માં ઇલેક્ટ્રોન ની સંખ્યા શું હશે ?View Solution
- 5નીચેનામાંથી ક્યા સમઇલેક્ટ્રોનિક અને સમબંધારણીય છે $NO_3^ - ,\,CO_3^{2 - },\,ClO_3^ - ,\,S{O_3}$View Solution
- 6${10^{ - 6}}\,kg$ દળ અને $10\,\,m{s^{ - 1}}$ ની વેગ સાથે ફરતા દ્દ-બ્રોગલી તરંગલંબાઇ શું હશે ?View Solution
- 7જો નાઈટ્રોજન પરમાણુમાં ઈલેકટ્રોનીક વિન્યાસ $1s^7$ છે, તેની ઊર્જા સામાન્ય ભૂમિ અવસ્થાના વિન્યાસ $1s^2 2s^2 2p^3, $કરતાં ઓછી છે. કારણ કે ઈલેકટ્રોન કેન્દ્રની નજીક આવેલું છે. તેથી $1s^7$ જોવા મળતી નથી. નીચેના પૈકી કયા નિયમનું પાલન કરતો નથી.View Solution
- 8નીચેનામાંથી ${O^{2 - }}$ સાથે ક્યુ આયન સમઈલેકટ્રોનિક નથી .View Solution
- 9View Solutionનીચે પૈકી હાઈડ્રોજન પરમાણુના ઊર્જા સ્તરો વચ્ચેના ઈલેકટ્રોનના સંક્રમણમાંથી કયા સંક્રમણમાં હાઈડ્રોજન વર્ણપટ્ટની સૌથી ટૂંકી તરંગ લંબાઈ ધરાવતી રેખા ઉત્પન્ન થાય છે ?
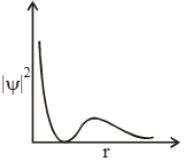
- 10${\left| \psi \right|^2}$ અને $r$(radial distance) વચ્ચેનો આલેખ નીચે દર્શાવ્યો છે . તે .. . રજૂ કરે છે .View Solution