Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1$32^{\circ} \mathrm{C}$ પ૨ $500 \mathrm{~mL}$ દ્રાવણ માં $x \mathrm{~g}$ નિર્જળ $\mathrm{CuSO}_4$ ધરાવતા એક જલીય દ્રાવણ ની મોલારિટી (M). $2 \times 10^{-1} \mathrm{M}$ છે. તો તેની મોલાલિટી. . . . . . . .$\times 10^{-3} \mathrm{~m}$ થશે. (નજીકનો પૂણાંક)View Solution
$d$દ્રાવણ $=1.25 \mathrm{~g} / \mathrm{mL}]$
- 2$3\ \mathrm{M}\ \mathrm{NaOH}$ (સૂત્ર ભાર $40 \mathrm{~g} \mathrm{~mol}^{-1}$ ) નું કદ કે જેને $\mathrm{NaOH}$ ના $84 \mathrm{~g}$ માંથી બનાવી શકાય છે. તે__________ $\times 10^{-1} \mathrm{dm}^3$.View Solution
- 3$500 \mathrm{~mL}$ પાણીમાં $5.85 \mathrm{~g}, \mathrm{NaCl}$ ધરાવતા એક જલીય દ્રાવણ ની મોલારિટી $(M)$ શોધો. (આપેલ : મોલર દળ $\mathrm{Na}: 23$ અને $\mathrm{Cl}: 35.5 \mathrm{gmol}^{-1}$ )View Solution
- 4$70 \%$ દલથી ટકાવારી ($sp. gravity$ $=1.54 \mathrm{~g} \mathrm{~cm}^{-}$3) ધરાવતા $1L$ ઓર્થોફોસ્ફોરીક એસીડની $\left(\mathrm{H}_3 \mathrm{PO}_4\right)$ મોલારીટી $M$ છે.) $\left(\mathrm{H}_3 \mathrm{PO}_4\right.$ નું મોલર દળ $\left.=98 \mathrm{~g} \mathrm{~mol}^{-1}\right)$View Solution
- 5$9$ mole પાણીમાં $1$ mole ઈથાઈલ આલ્કોહોલ ઉમેરીને એક દ્રાવણ બનાવવામાં આવ્યુ. દ્રાવણણાં દ્રાવ્ય ની દળ ટકાવારી. . . . . . . . .છે. (પૂણાંકમાં જવાબ)View Solution
(આપેલ : મોલર દળ $\mathrm{g} \mathrm{mol}^{-1}$ છે. ઈથાઈલ આલ્કોહોલ : $46$, પાણી : $18$)
- 6$\mathrm{H}_2 \mathrm{SO}_4$ નું એક દ્રાવાણ જે દળ વડે $31.4 \% \mathrm{H}_2 \mathrm{SO}_4$ અને $1.25 \mathrm{~g} / \mathrm{mL}$ ઘનતા ધરાવે છે. તો $\mathrm{H}_2 \mathrm{SO}_4$ દ્રાવણની મોલારિટી________$M$ છે.(નજકનો પૂણાંક) [આપેલ $\mathrm{H}_2 \mathrm{SO}_4$ નું મોલર દળ = $98 \mathrm{~g} \mathrm{~mol}^{-1}$ છે.]View Solution
- 7$\mathrm{NaCl}$ ના $3 \mathrm{M}$ જલીય દ્રાવણની મોલાલિટી (m) શોધી :View Solution
(આપેલ ) દ્રાવણની ધનતા $=1.25 \mathrm{~g} \mathrm{~mL}^{-1}$, મોલર દળ $\mathrm{g} \mathrm{mol}^{-1}: \mathrm{Na}-23, \mathrm{Cl}-35.5$ )
- 8$\mathrm{NaOH}$ ના $'x' M$ દ્રાવણ ($'x'$ મોલર) ની ધનતા $1.12 \mathrm{~g} \mathrm{~mL}{ }^{-1}$ છે, જ્યારે મોલાલીટીમાં, દ્રાવણની સાંદ્રતા $3 \mathrm{~m}$ ($3$ મોલલ) છે. તો $x$ શોધો.View Solution
(આપેલ: $\mathrm{NaOH}$ નું મોલર દળ $40 \mathrm{gmol}^{-1}$ છે.)
- 9ગ્લુકોઝ $\left(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6\right)$ નું દહન કરવાથી $\mathrm{CO}_2$ અને પાણી ઉત્પન્ન થાય છે. $900 \mathrm{~g}$ ગ્લુકોઝ નાં સંપૂર્ણ દહન માટે જરૂરી ઓકસીજન નો જથ્થો ($g$ માં ) શોધો.View Solution
[આપેલ: ગ્લુકોઝ નુ મોલર દળ $\mathrm{g} \mathrm{mol}{ }^{-1}$ મા $180$ છે.]
- 10View Solutionજથ્થો કે જે તાપમાન સાથે બદલાય (ફેરફાર) થાય છે તે________.
- 11View Solutionડાલ્ટન પરમાણ્વીય સિદ્ધાંત ના સંદર્ભ ખોટુ વિધાન પસંદ કરો.
- 12યુરિયાના જલીય દ્રાવણની મોલાલિટી $4.44 \mathrm{~m}$ છે. દ્રાવણમાં યુરિયા નો મોલ અંશ $x \times 10^{-3}$ છે. $x$ નું મૂલ્ય. . . . . . .(પૂર્ણાંક માં જવાબ)View Solution
- 13સંપૂર્ણ દહન કર્યા પછી $11 \mathrm{~g} \mathrm{CO}_2(\mathrm{~g})$ ઉતપન્ન કરવા માટે જરૂરી મિથેનના moles ની સંખ્યા શોધો. ( આપેલ : મિથેનનું મોલર દળ $\mathrm{g} \mathrm{mol}^{-1}: 16$ છે.)View Solution
- 14એક પદાર્થ $'A'$ ને $'B'$ અને $'C'$ ના મિશ્રાણના દ્રાવાણમાં તેમના $n_A, n_B$ અને $n_C$ $moles$ ની સંખ્યાના સંદર્ભમાં ઓગાળવામાં આવે છે. તો દ્રાવાણમાં $C$ ના મોલ અંશ શોધો.View Solution
- 15નીચે આપેલા પ્ર્ક્રિયા ને ધ્યાન માં લો .View Solution
$3 \mathrm{PbCl}_2+2\left(\mathrm{NH}_4\right)_3 \mathrm{PO}_4 \rightarrow \mathrm{Pb}_3\left(\mathrm{PO}_4\right)_2+6 \mathrm{NH}_4 \mathrm{Cl}$
જો $ \mathrm{PbCl}_2 $ ના $ 72 \mathrm{~m} \mathrm{~mol} \mathrm{ને}\left(\mathrm{NH}_4\right)_3 \mathrm{PO}_4 $ ના $ 50 \mathrm{~m}$
$\mathrm{mol}$ સાથે મિશ્ર કરવામાં આવે તો, બનતા $\mathrm{Pb}_3\left(\mathrm{PO}_4\right)_2$
નો જથ્થો ................... $m\ mol$ છે. (નજીકનો પૂણાંક)
- 16$\mathrm{CaCO}_3$ અને $\mathrm{MgCO}_3$ ના મિશ્રણનું વજન $2.21 \mathrm{~g}$ છે. જેને ગરમ કરતાં $1.152$ ગ્રામ પદાર્થ બાકી રહે છે. તો મિશ્રણનું બંધારણ શોધો. $\left(\mathrm{CaCO}_3\right.$ અને $\mathrm{MgCO}_3$ ના અ-ભાર અનુક્રમે $100,$ $84 \mathrm{~g} / \mathrm{mol})$View Solution
- 17એક કાર્બનિક સંયોજન $42.1 \%$ કાર્બન, $6.4 \%$ હાઈડ્રોજન અને બાકીના ઓક્સિજન ધરાવે છે. જે તેનું આણ઼વીય દળ (વજન) $342$ હોય તો તેનું અણુસૂત્ર શોધો :View Solution
- 18ડાલ્ટન ના પરમાણવીય સિધ્ધાંત ની ખોટી ધારણા/ઓ શોધો.View Solution
$(A)$ જુદા જુદા તત્વો ના પરમાણુઓ ના દળ જુદા જુદા (અલગ) હોય છે.
$(B)$ દ્રવ્ય (Matter) વિભાજ્ય પરમાણુઓનું બનેલું છે.
$(C)$ જુદા જુદા તત્વ ના પરમાણુઓ જ્યારે કોઈ નિશ્વિત પ્રમાણમાં (ગુણોત્તરમાં) જોડાય છે ત્યારે સંયોજનો બને છે.
$(D)$ આપેલ તત્વના બધા જ પરમાણુ જુદા જુદા ગુણધર્મો ધરાવે છે તેમાં દળનો પણ સમાવેશ થાય છે.
$(E)$ રાસાયણિક પ્રક્રિયામાં પરમાણુઓની ફેરગોઠવણીનો સમાવેશ થાય છે.
નીચે આપેલ વિકલ્પોમાંથી સાચું જવાબ પસંદ કરો.
- 19સંપૂર્ણ દહન કર્યા બાદ $22 \mathrm{~g} \mathrm{CO}_2$ ને ઉત્પન્ન કરવા માટે મિથેનનું જરૂરી દળ _________$\mathrm{g}$ છે. (મોલરદળ $\mathrm{g} \mathrm{mol}^{-1}$ માં આપેલ છે $\mathrm{C}=12.0$ $ \mathrm{H}=1.0 $ $ \mathrm{O}=16.0)$View Solution
- 20કાર્બોનેટ $\left( M _2 CO _3\right)$ ના $1\,g$ ની વધુ પ્રમાણમાં $HCl$ સાથે પ્રક્રિયા કરતાં $CO _2$ ના $0.01\,mol$ ઉત્પન્ન કરે છે. તો $M _2 CO _3$ નું મોલર દળ $.......\,g\,mol ^{-1}$ છે.View Solution
- 21જો $BaCl _2$ ના $5\,moles$ ને $Na _3 PO _4$ ના $2\,moles$ સાથે મિશ્ર કરવામાં આવે તો,બનતા $Ba _3\left( PO _4\right)_2$ ના $moles$ ની મહત્તમ સંખ્યા $........$ છે.(નજીકનો પૂર્ણાક)View Solution
- 22ધારી લો કે નીચે આપેલા સમીકરણ પ્રમાણે કાર્બન સળગે છે.View Solution
$2 C _{( s )}+ O _{2( g )} \rightarrow 2 CO_{( g )}$
જ્યારે $12\,g$ કાર્બન $48\,g$ ઓકિસજનમાં સળગે છે તો ઉતપન્ન થાય કાર્બન મોનોક્સાઈડ નું કદ $STP$ પર $..........\times 10^{-1}\,L$ થાય (પૂર્ણાંક માં જવાબ)
[આપેલ : $CO$ ને આદર્શ વાયુ ધારી લો પરમાણ્વીય દળ $C$ નું $124$,$O$ નું $164$ અને $STP$ પર એક આદર્શ વાયુ મોલર કદ $22.7\,L\,mol ^{-1}$ છે.]
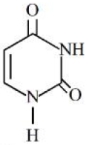
- 23નીચે આપેલ બંધારણ સાથે $RNA$ માં હાજર યુરેસીલ બેઇઝ છે. યુરિસિલમાં $N$ ના $\%............$ છે.View Solution
મોલર દળ $N =14\,g\,mol ^{-1} ; O =16\,g\,mol ^{-1} ; C =12\,g\,mol ^{-1} ; H =1\,g\,mol ^{-1}$;
- 24$0.69\,g$ ધાત્વિક સોડિયમને પાણી સાથે પ્રક્રિયા કરી મળેલા $NaOH$ ના સંપૂર્ણ તટસ્થીકરણ કરવા માટે જરૂરી $73\,g\,L ^{-1}$ વાળા $HCL$નું કદ $........mL$ છે.View Solution
(આપેલ : $Na, Cl, O$ અને $H$ નું મોલર દળ અનુક્રમે $23,35.5,16$ અને $1$ છે.) - 25$20\,mL$ કેલ્શિયમ હાઈડ્રોકસાઈડ વપરાય છે જ્યારે તેને તેની પ્રક્રિયા $10\,mL\,H _2 SO _4$ ના અજ્ઞાત દ્રાવણ સાથે પ્રક્રિયા કરવામાં આવે છે.આ ઉપરાંત ફિનોલ્ફથેલીનના $2$ ટીપાંઓ ધરાવતા $0.5\,M\,HCl$ ના $20\,mL$ પ્રમાણિત દ્રાવણનું કેલ્શિમ હાઇડ્રોકસાઈડ સાથે અનુમાપન કરવામાં આવે છે.મિશ્રણ ગુલાબી રંગ દર્શાવે છે જ્યારે બ્યુરેટ $35.5\,mL$ નું મૂલ્ય દર્શાવ્યું હતું જ્યાં બ્યુરેટ શરૂઆતમાં (પ્રારંભમાં) $25.5\,mL$ દર્શાવ્યું હતું.તો $H _2 SO _4$ ની સાંદ્રતા $......\,M$ છે.(નજીકનો પૂર્ણાક)View Solution
- 26$500\,g\,0.25\,molar$ જલીય દ્રાવણ અને $250\,mL 0.25\,molar$ જલીય દ્રાવણ બનાવવા માટે ઈથિલિન ગ્લાયકોલ $\left( C _2 H _6 O _2\right.$, મોલર દળ = $\left.62\,g / mol \right)$ નો કેટલો દળ ગુણોત્તર જરૂરી છે ?View Solution
- 27$5\,g\,NaOH$ ને વિઆાયોનિક પાણી $(deionized\,water)$ માં આોગાળીને બલ્ક દ્રાવણ $(stock\,solution)$ બનાવવામાં આવ્યું. આ દ્રાવણ નું કેટલું કદ $(mL$ માં) $0.1\,M$ નું $500\,mL$ દ્રાવણ બનાવવા માટે જરૂરી બનશે ? આપેલ : $Na , O$ અને $H$ નું મોલર દળ અનુક્રમે $23,16$ અને $1\,g\,mol ^{-1}$ છે.View Solution
- 28$60 \%$ કાર્બન ધરાવતા, એક કાર્બનિક સંયોજના $0.01$ મોલને સંપૂર્ણ બાળવામાં આવે ત્યારે $4.4\,g\, CO_2$ ઉત્પન્ન થાય છે. તો સંયોજનનું મોલર દળ $..............g\,mol ^{-1}$ છે.(નજીકના પૂર્ણાંકમાં)View Solution
- 29$CCl_4$ (કાર્બન ટેટ્રાક્લોરાઈડ) માં ડાય-બ્રોમિનના $10\% (v/v)$ દ્રાવણની મોલાલિટી $x$ છે.તો $x=...... \times 10^{-2}\,M$. (નજીકનો પૂર્ણાંક)View Solution
[આપેલ $Br_2$ નું મોલર દળ $=160\,g\,mol^{-1}$
$C$ નું પરમાણ્વિય દળ = $12\,g\,mol^{-1}$
$Cl$ નું પરમાણ્વિય દળ = $35.5\,g\,mol^{-1}$
ડાય-બ્રોમિનની ઘનતા = $3.2\,g\,mL^{-1}$
$CCl_4$ ની ઘનતા = $1.6\,g\,mL^{-1}$]
- 30$\left[ Cr \left( H _2 O \right)_5 Cl] Cl _2\right.$ ના $0.01\,M$ દ્રાવણના $20\,mL$ માં હાજર કલોરાઈડ આયનોના સંપૂર્ણ અવક્ષેપન સિલ્વર કલોરાઇડ તરીકે કરવા માટે $0.1\,M\,AgNO _3$ નું જરૂરી કદ $(mL$ માં) $.......$ છે.View Solution
- 31$STP$ પર $O _2$ ના $2.8375\,liters$ માં અણુઓ અને $moles$ ની સંખ્યા અનુક્રમે શોધો.View Solution
- 32એક કાર્બનિક સંયોજનનું સંપૂર્ણ દહન કરતાં તે $0.220\,g\,CO _2$ અને $0.126\,g\,H _2 O$ આપે છે.જો કાર્બનના $\%$ એ $24 \%$ હોય તો પછી હાઈડ્રોજનના $\%$ $........\,\times 10^{-1}$ છે.(નજીકનો પૂર્ણાક)View Solution
- 33એક ધાતુ કલોરાઈડ કલોરીનના $55.0 \%$ દળ થી (વજનથી) ધરાવે છે.$STP$ પર ધાતુ કલોરાઈડની $100\,mL$ બાષ્પ $0.57\,g$ વજન ધરાવે છે.ધાતુ કલોરાઈડનું અણુસૂત્ર શોધો. (આપેલ : કલોરિનનું પરમાણ્વીય દળ $35.5\,u$ છે.)View Solution
- 34એક મોનોબેઝિક પ્રબળ એસિડ (મોલર દળ $24.2\,g / mol$) ની ધનતા $1.21\,kg\,L$ છે. તો $25\,mL\,0.24\,M$ $NaOH$ નું સંપૂર્ણ તટસ્થીકરણ કરવા માટે તેના દ્રાવણનું કદ $........\times 10^{-2}\,mL$ છે. (નજીકનો પૂર્ણાંક)View Solution
- 35જયારે એક હાઇડ્રોકાર્બન $A$નું સંપૂર્ણ દહન થાય છે ત્યારે ઓકિસજનના $11$ તુલ્યાંકની જરૂર પડે છે અને પાણીના $4$ તુલ્યાંક ઉત્પન્ન કરે છે. તો $A$ નું અણુસુત્ર શું છે ?View Solution
- 36ઝિંકની હાઈડ્રોક્લોરિક એસિડ સાથે પ્રક્રિયા કરતાં તે હાઈડ્રોજન અને ઝિંક ક્લોરાઇડ આપે છે. $11.5\,g$ ઝિંક સાથે વધુ પ્રમાણમાં $HCl$ સાથે પ્રક્રિયા કરતા તેમાંથી ઉત્પન્ન થતા હાઈડ્રોજન વાયુનું કદ $STP$ એ $.........L$ છે. (આપેલ :$Zn$નું મોલર દળ $65.4\,g\,mol ^{-1}$ છે.) (નજીકનો પૂર્ણાંક)View Solution
- 37ઠંડા પીણાની $300\,mL$ ની બાટલીમાં $0.2\,M\,CO_2$ ઓગાળેલો છે.ધારી લઈએ કે $CO_2$આદર્શ વાયુ તરીકે વર્તે છે,તો $STP$ એ ઓગાળેલા $CO_2$ વાયુનું કદ $.........\,ml$ છે.(નજીકનો પૂર્ણાંક)(આપેલું છે. : $STP$ એ એક આદર્શ વાયુનું મોલર કદ $22.7\,L\,mol^{-1}$)View Solution
- 38નીચે આપેલ પ્રક્રિયાઓ માં, $X$ અને $Y$ માં ઓકિસજન પરમાણુઓની કુલ સંખ્યા $........$ છે.View Solution
$Na _2 O + H _2 O \rightarrow 2 X$
$Cl _2 O _7+ H _2 O \rightarrow 2 Y$
- 39નીચે આપેલામાંથી કયો અર્થસૂચક (સાર્થક) અંકોની સમાન સંખ્યા દર્શાવે છે.View Solution
(A) $0.00253$ (B) $1.0003$ (C) $15.0$ (D) $163$
નીચે આપેલા વિકલ્પોમાથી સાચો જવાબ પસંદ કરો.
- 40સૂચિ $I$ સાથે સૂચિ $II$ ને જોડો.View Solution
સૂચિ $I$ સૂચિ $II$ $A$ $CH _{4( g )}$ ના $16\,g$ $I$ વજન $28\,g$ $B$ $H _{2( g )}$ ના $1\,g$ $II$ $60.2 \times 10^{23}$ ઇલેક્ટ્રોન્સ $C$ $N _{2( g )}$ ના $1\,mole$ $III$ વજન $32\,g$ $D$ $SO _{2( g )}$ ના $0.5\,mol$ $IV$ $STP$ પર $11.4\,L$ કદ રોકે છે. નીચે આપેલા વિકલ્પોમાથી સાચો જવાબ પસંદ કરો.
- 41$56.0\, L$ નાઈટ્રોજન વાયુને વધુ પડતા હાઈડ્રોજન વાયુ સાથે મિશ્ર કરવામાં આવે છ અને જોવા મળ્યું કે $20\, L$ એમોનિયા વાયુ ઉત્પન્ન થાય છે. તો મળી આવેલ વણવપરાયેલ (વપરાયેલ ન હોય તેવો) નાઈટ્રોજન વાયુ $.....\,L$ છે.View Solution
- 42આપેલ પ્રક્રિયા માંView Solution
$X+Y+3 Z \leftrightarrows X Y Z_{3}$
$X$ અને $Y$ દરેકના એક $mol$ સાથે $Z$ ના $0.05 \,mol$ એ $XYZ _{3}$ સંયોજન આપે છે તો $XYZ _{3}$ નીપન ......... $g$ છે. (આપેલ : $X, Y$ અને $Z$ ના પરમાણ્વિય દળો અનુક્રમે $10, 20$ અને $30 \,amu$ છે. ) ( ના જુ ક ના પૂર્ણાંકમાં)
- 43જ્યાંરે $0.01\, M\, KMnO _{4}$ દ્રાવણ ને $20.0 \,mL\,\, 0.05\, M$ મ્હોર દ્રાવણમાં બ્યુરેટ દ્વારા ઉમેરવામાં આવ્યું. $50\, mL$ બ્યુરેટ નું પ્રારંભિક અવલોકન શૂન્ય છે. અંતિમ બિંદુ બાદ બ્યુરેટમાં બાકી રહેલા $KMnO _{4}$ નું ક્દ......... $mL$ (નજીકના પૂર્ણાકમાં)View Solution
- 44જ્યારે $10\,mL\,0.1\,M$ એસિડ $'A'$ ને $30\,mL\,0.05\,M$ બેઇઝ $M(OH)_2$ સાથે પ્રક્રિયા કરવા દેવામાં આવે તો તટસ્થીકરણ પ્રક્રિયા થાય છે. એસિડ $'A'$ ની બેઝિકતા $\dots\dots$છે. $[M$ એ ધાતુ છે$]$View Solution
- 45અર્થસૂચક સંખ્યાના નિયમનો ઉપયોગ કરી, નીચે આપેલાના સંદર્ભમાં સાચો જવાબ શું હશે ?View Solution
$\frac{0.02858 \times 0.112}{0.5702}$
- 46$116\, g$ ક્રિયાધર (substance)ની વિયોજીત પ્રક્રિયા થઈ $7.5 \,g$ હાઈડ્રોજન, $60\, g$ ઓકિસજન, $48.5 \,g$ કાર્બન આપે છે. આપેલ $H, \,O$ અને $C$ ના પરમાણ્વીયભાર અનુક્રમે $1,16,12$ છે.તો આપેલમાંથી કેટલા સૂત્રો આ માહિતી સાથે સંમત થશે $?$View Solution
$(A)$ $CH _{3} COOH$
$(B)$ $HCHO$
$(C)$ $CH _{3} OOCH _{3}$
$(D)$ $CH _{3} CHO$
- 47$120\,g$ એક કાર્બનિક સંયોજન જે ફક્ત કાર્બન અને હાઈડ્રોજન ધરાવે છે જ્યારે તેનું સંપૂર્ણ દહન કરવામાં આવે તો તે $330\,g\,\,CO _{2}$ અને $270\,g$ પાણી આપે છે. કાર્બન અને હાઈડ્રોજનની ટકાવારી અનુક્રમે શોધો.View Solution
- 48$250 \,g$ $D$-ગ્લુકોઝના જલીય દ્રાવણમાં $10.8\%$ વજનથી કાર્બન છે. તો દ્રાવણની મોલાલીટી ................ છે. (નજીક છે તે) આપેલું છે : પરમાણુ દળાંક $H,1;C,12;O,16$ )View Solution
- 49$2\,L\,0.2\,M H _{2} SO _{4}$ ની $2\,L\, \ 0.1\,M$ $NaOH$ દ્વાવણ સાથે પ્રક્રિયા કરતા, દ્રાવણમાં બનતી પરિણામી નીપજ $Na _2 SO _4$ ની મોલારીટી $.........$ મિલિમોલર છે. (નજીકનો પૂર્ણાંક)View Solution
- 50$5\,g$ પેન્ટ$-1-$ઈન $\left( C _{5} H _{10}\right)$ સાથે સંપૂર્ણ પ્રક્રિયા થવા માટે બ્રોમિનના ગ્રામની સંખ્યા $\dots\dots\dots\times 10^{-2}$ grams છે.$(Br$ નો પરમાણ્વીય. દળ $=80\,g / mol$ )View Solution
- 51$81\,\,g\,\,H _{2} O$ ઉત્પન્ન કરવા માટે દહન બાદ મિથેનના $\dots\dots\dots\times 10^{-2} mol$ ની જરૂર પડે છે.View Solution
- 52$C _{7} H _{5} N _{3} O _{6}$ ના $681\,g$ માં $N$ પરમાણુઓની સંખ્યા $x \times 10^{21}$ છે. તો $x$ નું મૂલ્ય $.....$ છે.View Solution
$( N _{ A }=6.02 \times 10^{23} \,mol ^{-1})$(નજીકનો પૂર્ણાંક)
- 53$CNG$ એક અગત્યનો વાહન વ્યવહારનું બળતણ છે. જ્યારે $100\,g\,CNG$ ને $208\,g$ ઓકિસજન સાથે વાહનમાં નાખવામાં આવે ત્યારે $CO _{2}$ અને $H _{2} O$ બનવા તરફ દોરી જાય છે અને વધુ પ્રમાણમાં ઉષ્મા ઉત્પન્ન આ દહન દરમયાન ઉત્પન્ન થતો $CO _{2}$ નો જથ્થો (ગ્રામમાં) $\dots\dots\dots$ છે.[ધારી લો $CNG =$મિથેન]View Solution
- 54$H _{2} SO _{4}$ નું $1\,L$ જલીય દ્રાવણ $0.02\,m\,mol \,H_{2}SO _{4}$ ધરાવે છે. આ દ્રાવણમાંથી $50 \%$ ને નિસ્યંદિત પાણી વડે મંદ કરીને $1\,L$ દ્રાવણ $(A)$ બનાવવામાં આવે છે. દ્રાણણ $(A)$ માં $H _{2} SO _{4}$ ના $0.01\,m\,mol$ ઉમેરવામાં આવે છે. તો અંતિમ દ્રાવણમાં $H _{2} SO _{4}$ ના કુલ $m\,mols\dots\dots\dots$ $\times 10^{3} \,m\, mols$ છે.View Solution
- 55$N _{2( g )}+3 H _{2( g )} \rightleftharpoons 2 NH _{3( g )}$View Solution
$20 \;g \;\;\;\;5 \;g$
ઉપરની પ્રક્રિયાને ધ્યાનમાં લો. પ્રક્રિયાનો મર્યાદિત પ્રક્રિયક અને $NH _3$ ના બનતા $moles$ની સંખ્યા અનુક્રમે શોધો.
- 56$SO _2 Cl _2$ ને વધુ પડતા પાણી સાથે પ્રક્રિયા કરતા એસિડિક મિશ્રણ માં પરિણમે છે.View Solution
$SO _{2} Cl _{2}+2 H _{2} O \rightarrow H _{2} SO _{4}+2 HCl$
આ પરિણામી એસિડિક મિશ્રણને તટસ્થ કરવા માટે જો $16$ મોલ $NaOH$ જરૂરી હોય તો વપરતા $SO _2 Cl _2$ ના મોલની, સંખ્યા?
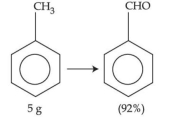
- 57ઉપરની પ્રક્રિયામાં $5\, g$ ટોલ્યુઈનનું $92\, \%$ સાથેના બેન્ઝાલ્ડીહાઈડ નીપજમાં પરિવર્તન થાય છે. ઉત્પન્ન થયેલ બેન્ઝાલ્ડીહાઈડનો જથ્થો $........\,\times 10^{-2}\, g$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
- 58એક અજ્ઞાત મોનોહાઈડ્રીક આલ્કોહોલ, $R-OH$ ના $4.5\, mg$ નો એક નમૂનાને મિથાઈલ મેગ્નેશિયમ આયોડાઈડમાં ઉમેરવામાં આવે છે. નીકળતા વાયુને ભેગો કરી તેનું કદ $3.1\,mL$ માપવામાં આવ્યું, તો અજ્ઞાત આલ્કોહોલનો અણુભાર $........\,g / mol$ છે. (નજીકનો પૂર્ણાંક)View Solution
- 59એક પ્રોટીન $'A'$ એ $0.30 \%$ ગ્લાયસીન $($અણુભાર $75)$ ધરાવે છે. પ્રોટીન $'A'$ નો ઓછામાં ઓછો અણુભાર $\dots\dots\dots\times 10^{3}\,g\,mol ^{-1}$. [નજીકનો પૂર્ણાંક]View Solution
- 60એક સંયોજન $A$ $8.7 \%$ હાઈડ્રોજન, $74 \%$ કાર્બન અને $17.3 \%$ નાઈટ્રોજન ધરાવે છે. સંયોજન $A$ નું મોલર દળ $162\, g\, mol ^{-1}$ છે. સંયોજનનું અણુસૂત્ર શોધો.View Solution
આપેલ : કાર્બન, હાઈડ્રોજન અને નાઈટ્રોજન ના પરમાણ્વીય દળો અનુક્રમે $12,\, 1$ અને $14 \, amu$ છે.
- 61જો એક રોકેટ એ બળતણ $\left( C _{15} H _{30}\right)$ અને પ્રવાહી ઓક્સિજન પર ગતિ (દોડે) કરે છે.જરૂરી ઓક્સિજનનું વજન અને બળતળ ના દરેક લિટરે મુક્ત થતો $CO_{2}$ અનુક્રમે શોધો:(આપેલ:બળતળની ઘનતા $0.756\,g/ml$ છે.)View Solution
- 62જ્યારે $0.5 \,M$ નાઈટ્રિક એસિડના $800 \,mL$ ને બીકરમાં ગરમ કરવામાં આવે ત્યારે તેનું કદ ઘટીને અડધું થાય છે અને $11.5\, g$ નાઈટ્રિક એસિડનું બાષ્પીભવન થાય છે. બાકી રહેલા નાઈટ્રિક એસિડની મોલારિટી $x \times 10^{-2} \,M$ છે. તો $x$ નું મુલ્ય $......$ છે. (નજીકનો પૂર્ણાંક )View Solution
(નાઈટ્રિક એસિડનું મોલર દળ $63 \,g \,mol ^{-1}$ છે.)
- 63જ્યારે $200\,mL\,0.2\,M$ એસિટીક એસિડને $0.6\,g$ લાકડાના કોલસા સાથે હલાવામાં આવે છે.ત્યારે અધિશોષણ બાદ એસિટીક એસિડનું અંતિમ સાંદ્રતા $0.1\, M$છે કાર્બનના પર ગ્રામ ઉપર અધિશોષિત એસિટીક એસીડનું દળ $\dots\dots\dots\,g$View Solution
- 64નીચે બે વિધાનો આપેલા છે. એકને વિધાન $(A)$ અને બીજાને કારણ $(R)$ તરીકે દર્શાવ્યું છે.View Solution
વિધાન $(A) :\,10^{\circ} C$ એ $5\, M\, KCl$ ના દ્રાવણની ઘનતા $'x^{\prime} g\, ml ^{-1}$ છે. [ $K$ અને $Cl$ નો પરમાણ્વીય દળો ક્રમશ: $39$ અને $35.5\, g\, mol ^{-1}$ છે.] દ્રાવણને $-21^{\circ} C$ એ ઠંડુ કરવામાં આવે છે. દ્રાવણની મોલાલિટી બદલાતી નથી.
કારણ $(R) :$ દ્રાવણની મોલાલિટી તાપમાન સાથે બદલાતી નથી, કારણ કે દળ તાપમાન સાથે બદલાતું નથી.
ઉપરોક્ત વિધાનોના સંદર્ભે, આપેલા વિકલ્પમાંથી યોગ્ય ઉત્તર ની પસંદગી કરો.
- 65પ્રક્રિયાને ધ્યાનમાં લો,View Solution
$4 HNO _{3}(l)+3 KCl ( s ) \rightarrow Cl _{2}( g )+ NOCl ( g )+ 2 H _{2} O ( g )+3 KNO _{3}( s )$
$110.0\, g \,KNO _3$ નું ઉત્પાદન કરવા $HNO _3$ ની જરૂરી માત્રા $...... \;g$ શોધો.
(આપેલ : પરમાણ્વીય દળ $H : 1, O : 16, N : 14$ અને $K : 39)$
- 66વાટેલા લીલા પાંદડાઓમાંથી નિષ્કર્ષણ કરેલ ક્લોરોફિલને પાણીમાં ઓગાળી ને $48\, ppm\, Mg$ની સાંદ્રતાવાળું $2\, L$ દ્રાવણ બનાવ્યું. આ દ્રાવણમાં $Mg$ ના પરમાણુઓની સંખ્યા $x \times 10^{20}$ પરમાણુઓ છે. $x$ નું મૂલ્ય $.....$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : $Mg$ નો પરમાણ્વીય દળ $24\, g\, mol ^{-1} ; N _{ A }=6.02 \times 10^{23}\, mol ^{-1}$ )
- 67વાતભઠ્ઠીમાં આયર્નનું ઉત્પાદન નીચે આપેલા સમીકરણને અનુસરે છે.View Solution
$Fe _{3} O _{4}( s )+4 CO ( g ) \rightarrow 3 Fe ( l )+4 CO _{2}( g )$
જયારે $4.640\,kg\,Fe _{3} O _{4}$ અને $2.520\,kg\,CO$ ને પ્રક્રિયા કરવા દેવામાં આવે તો ત્યારે પછી ઉત્પન્ન થતા આયર્નનો જથ્થો શોધો :
[આપેલ : $\quad Fe$ નું પરમાણ્વીય દળ $=56\,g\,mol ^{-1}$
$O$નું પરમાણ્વીય દળ$=16\,g\,mol ^{-1}$
$C$ નું પરમાણ્વીય દળ $=12\,g\,mol ^{-1}$ ]
- 68વ્યાપારિક ધોરણે વેચાતો સાંદ્ર $HCl$ એ દળથી $35\%$ $HCl$ છે.જો આ વ્યાપારિક એસિડની ઘનતા $1.46\,g / mL$ હોય તો,આા દ્રાવણની મોલારિટી શું છે?View Solution
- 69હિમોગ્લોબીન $0.34 \,\%$ આર્યન દળથી ધરાવે છે. તો $3.3\, g$ હિમોગ્લોબીનમાં $Fe$ પરમાણુઓની સંખ્યા શોધો.View Solution
(આપેલ : પરમાણ્વીય દળ $Fe =56\, u , N _{ A }=6.022 \times 10^{23}\, mol ^{-1}$ )
- 70$10.0 \,{~mL}$ $0.05\, {M}\, {KMnO}_{4}$ દ્રાવણનો ઉપયોગ $10.0\, {~mL}$ આપેલા ઓક્ઝેલિક એસિડના ડાયહાઇડ્રેટ દ્રાવણ સાથે ટાઇટ્રેશનમાં કરવામાં આવ્યો હતો. આપેલા ઓક્ઝેલિક એસિડ દ્રાવણની સાંદ્રતા $.....\,\times 10^{-2} \,{~g} / {L}.$View Solution
- 71$100\, {~mL}$ ${Na}_{3} {PO}_{4}$ દ્રાવણમાં $3.45\, {~g}$ સોડિયમ છે. દ્રાવણની મોલારીટી $.....\times 10^{-2}$ $\operatorname{mol} \,{L}^{-1} \cdot($ નજીકના પૂર્ણાંકમાં $)$View Solution
[અણુ દળ - ${Na}: 23.0\, {u}, {O}: 16.0\, {u}, {P}: 31.0 \,{u}]$
- 72$10\, {~g}$ બેન્ઝીનનું મિથાઇલેશન પર $9.2\, {~g}$ ટોલ્યુઇન આપ્યું. ટોલ્યુઇન નીપજની ટકાવારીની ગણતરી કરો. (નજીકના પૂર્ણાંકમાં)View Solution
- 73$1.80\, g$ ઓક્સીજન ધરાવતું એક સંયોજન $\left( C _{x} H _{y} O _{z}\right)$ નું સંપૂર્ણ દહન કરતા $2.64\, g\, CO_2$ અને $1.08\, g\, H_2O$ આપે છે. તો કાર્બનિક સંયોજનમાં ઓક્સીજનની ટકાવારી .......... છે.View Solution
- 74$4.5 \,g$ સંયોજન $A (MW = 90)$ નો ઉપયોગ કરીને તેનું $250\, mL$ જલીય દ્રાવણ બનાવવામાં આવ્યું. દ્રાવણની મોલારિટી $M$ એ $x \times 10^{-1}$ છે. તો $x$ નું મૂલ્ય ........... છે. (નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)View Solution
- 75$50000.020 \times 10^{-3}$ માં અર્થસૂચક આંકડાઓની સંખ્યા ........... છે.View Solution
- 76$KOH$ $(aq.)$નું $6.50$ મોલલ દ્રાવણની ઘનતા $1.89\, g\, cm ^{-3}$ છે. દ્રાવણની મોલારિટી .......... $mol\, dm ^{-3}$છે.View Solution
[પરમાણ્વીય દળ: $K : 39.0\, u ; O : 16.0 \,u ; H : 1.0\, u ]$
- 77${NaOH}$ દ્રાવણની ઘનતા $1.2 \,{gcm}^{-3}$ છે. આ દ્રાવણની મોલારીટી $....\,m$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
[ઉપયોગ: પરમાણ્વીય દળ:$Na:23.0\,u {O}: 16.0 \,{u} \quad {H}: 1.0 \,{u}$, ઘનતા ${H}_{2} {O}: 1.0 \,{~g} \,{~cm}^{-3}$ ]
- 78$NaOH$ નાં દ્રાવણ વિરૂદ્ધ $1.25\, M$ ઓકઝેલિક એસિડ દ્રાવણના અનુમાપનને ધ્યાનમાં લો. અંતિમ બિંદુ પર નીચે મુજબ બ્યુરેટ અવલોકનો મળ્યાં.View Solution
$(i)$ $4.5\, mL$ $\quad (ii)$ $4.5\, mL$ $\quad (iii)$ $4.4\, mL$
$(iv)$ $4.4\, mL$ $\quad (v)$ $4.4\, mL$
જે ઓકઝેલિક એસિડનું કદ $10.0\, mL$ લેવામાં આવ્યું હોય તો $NaOH$ દ્રાવણની મોલારિટી $....\,M$ છે. (નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ કરો)
- 79જલીય ${KCl}$ દ્રાવણની ઘનતા $1.20 {~g} {~mL}^{-1}$ એ $3.30 {~mol} {~kg}^{-1}$ મોલાલીટી ધરાવે છે. દ્રાવણની મોલારિટી $.....$ ${mol} {L}^{-1}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
[મોલર દળ ${KCl}=74.5$ ]
- 80જ્યારે $10 {~mL}$ ${Fe}^{2+}$ આયનોના જલીય દ્રાવણને ડાયફિનાઇલએમાઇન સૂચકનો ઉપયોગ કરીને મંદ ${H}_{2} {SO}_{4}$ની હાજરીમાં ટાઇટ્રેટ કરવામાં આવ્યું હતું, , અંતિમ બિંદુ મેળવવા માટે $0.02 {M}$ ${K}_{2} {Cr}_{2} {O}_{7}$નું $15 {~mL}$ જરૂરી હતું. ${Fe}^{2+}$ આયનો ધરાવતા દ્રાવણની મોલારિટી ${X} \times 10^{-2} {M}$ છે. ${x}$ નું મૂલ્ય $....$ (નજીકનું પૂર્ણાંક) છે.View Solution
- 81બ્યુટેનના સંપૂર્ણ દહનને ધ્યાનમાં લો, $72.0\, {~g}$ પાણી પેદા કરવા માટે ઉપયોગમાં લેવાતા બ્યુટેનની માત્રા $....\,\times 10^{-1}\, {~g} .$ (નજીકના પૂર્ણાંકમાં )View Solution
- 82$\left({P}+\frac{{an}^{2}}{{~V}^{2}}\right)({V}-{nb})={n} {RT}$માં વાન ડર વાલ્સ વાયુ સમીકરણમાં પેરામીટર $'a'$નો એકમ છે:View Solution
- 83$NaNO _{3}$નું ...... $g$ વજન કરી અને તેનું $50 \,mL$ જલીય દ્રાવણ બનાવવામાં આવે કે જે $70.0\, mg$ પ્રતિ $mL$ $Na ^{+}$ ધરાવે. (નજીકનો પૂર્ણાંકમાં રાઉન્ડ ઑફ) (આપેલ : પરમાણ્વીય વજન $g\, mol ^{-1}$માં) $[Na : 23; N : 14 ; O : 16]$View Solution
- 84જો લોહીમાં ગ્લુકોઝ $\left({C}_{6} {H}_{12} {O}_{6}\right)$ની સાંદ્રતા $0.72\, {~g} \,{~L}^{-1}$, તો લોહીમાં ગ્લુકોઝની મોલરિટી $.....\,\times 10^{-3} {M}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
(આપેલ છે: આણ્વિય દળ ${C}=12, {H}=1, {O}=16 {u}$ )
- 85$0.5\, {M}\, {NaOH}$ $250\, {~mL}$ને $500\, {~mL}$ $1\, {M}\, {HCl}$ ઉમેરવામાં આવ્યુ છે. સંપૂર્ણ પ્રક્રિયા પછી દ્રાવણમાં બિનપ્રક્રિયકૃત ${HCl}$ પરમાણુની સંખ્યા $......\,\times 10^{21}$ છે. (નજીકના પૂર્ણાંકમાં) $\left({N}_{{A}}=6.022 \times 10^{23}\right)$View Solution
- 86$100\, {~g}$ પ્રોપેન સંપૂર્ણપણે $1000\, {~g}$ ઓક્સિજન સાથે પ્રક્રિયા આપે છે. પરિણામી મિશ્રણમાં કાર્બન ડાયોક્સાઇડનો મોલ અંશ ${x} \times 10^{-2}$ છે. ${x}$નું મૂલ્ય $.....$ છે.View Solution
[આણ્વિય વજન : ${H}=1.008 ; {C}=12.00 ; {O}=16.00$ ]
- 87$100$ મોલલ જલીય દ્રાવણમાં દ્રાવકનો મોલ અંશ ........... $\times 10^{-2}$View Solution
[આપેલ છે: આણ્વિય દળ : $H : 1.0 \,u , O : 16.0\, u$ ]
- 88$1 \,M \,H _{3} PO _{3}$ નાં $50 \,mL$ દ્રાવણ અને $2 \,M\, H _{3} PO _{2}$ નાં $100\, mL$ દ્રાવણને તટસ્થીકરણ કરવા $1\, M\, NaOH$ દ્રાવણનું ચોક્કસ કદ શોધો.View Solution
- 89$250\, {~mL}$ પાણીમાં $6.3\, {~g}$ ઓક્ઝેલિક એસિડ $\left({H}_{2} {C}_{2} {O}_{4} \cdot 2 {H}_{2} {O}\right)$ ઓગાળીને તૈયાર કરેલા દ્રાવણની મોલારિટી $\operatorname{mol} {L}^{-1}$ is ${x} \times 10^{-2}$ છે. ${x}$નું મૂલ્ય $.....$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
[આણ્વિય દળ : ${H}: 1.0, {C}: 12.0, {O}: 16.0]$
- 90$8\, {~g}$ સોડિયમમાં અણુઓની સંખ્યા ${x} \times 10^{23}$ છે. ${x}$નું મૂલ્ય $......$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
$\left[\right.$ આપેલ છે $: {N}_{{A}}=6.02 \times 10^{23}\, {~mol}^{-1}$ ,${Na}$નું આણ્વીય દળ $=23.0\, {u}]$
- 91ઇથેન ના $3\, g$ સંપૂર્ણ દહને પાણી ના $x \times 10^{22}$ અણું આપે છે $x$ ની કિંમત શોધો....... [ઉપયોગ કરો : $N _{ A }=6.023 \times 10^{23} ;$ આણ્વિય દળ $u$ $C : 12.0 ; O : 16.0 ; H : 1.0]$View Solution
- 92એક વાયુમય હાઈડ્રોકાર્બન કે જેના સંપૂર્ણ ઓક્સિડેશન થવા માટે પોતાના કદ કરતા $6$ ગણો વધારે $O _{2}$ ની જરૂરી છે અને ત્યારબાદ તેમાંથી ઉત્પન્ન થતો $CO _{2}$ પોતાના કરતા $4$ ગણું કદ ધરાવે છે તેનું સૂત્ર $C _{ x } H _{ y }$ છે. તો $y$ નું મૂલ્ય ....... છે.View Solution
- 93એસિડિક માધ્યમમાં $15\, mL$ $Fe ^{2+}$નું જલીય દ્રાવણ $20\, mL$ $0.03\, M$ જલીય $Cr _{2} O _{7}^{2-}$ સાથે સંપૂર્ણપણે પ્રક્રિયા આપે છે. $Fe ^{2+}$ દ્રાવણની મોલારિટી ........... $\times 10^{-2} M$ છે.View Solution
- 94જ્યારે $35\, mL \,0.15\, M$ લેડ નાઈટ્રેટ દ્રાવણને $0.12\, M$ ક્રોમિક સલ્ફેટનાં $20\, mL$ દ્રાવણ સાથે મિશ્ર કરવામાં આવે છે ત્યારે લેડ સલ્ફેટનાં ....... $\times 10^{-5}$ મોલ્સ (moles)નું અવક્ષેપન થશે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઓફ કરો)View Solution
- 95મોહર ક્ષાર અને પોટાશ ફટકડીમાં પાણીના અણુઓની સંખ્યાનો ગુણોત્તર $....\,\times 10^{-1}$ છે.View Solution
- 96સોડિયમ ઓક્સાઇડ સોડિયમ હાઇડ્રોક્સાઇડ ઉત્પન્ન કરવા પાણી સાથે પ્રક્રિયા આપે છે. $20.0\, {~g}$ સોડિયમ ઓક્સાઇડ $500\, {~mL}$ પાણીમાં ઓગળી જાય છે. કદમાં ફેરફારને અવગણો, પરિણામી ${NaOH}$ દ્રાવણની સાંદ્રતા $........\times \quad 10^{-1} \quad$ $M.$ (નજીકના પૂર્ણાંકમાં)View Solution
[આણ્વિય દળ $: {Na}=23.0, {O}=16.0, {H}=1.0]$
- 97$1^{\text {st }} $ઘટકના $n_{1}$ મોલ્સ અને $2^{\text {nd }}$ ઘટકના $n_{2}$ મોલ્સ ધરાવતા બે ઘટકોનો દ્રાવણ તૈયાર છે. ઘટક $1$ અને $2$ ના આણ્વિય દળ અનુક્રમે $M _{1}$ અને $M _{2}$ છે જો $2^{\text {nd }}$ ઘટકમાં $ d $ એ દ્રાવણમાં ઘનતા $g\, mL ^{-1}$ માં છે ,$C _{2}$ એ મોલારિટી છે અને $x _{2}$એ મોલ અંશ છે તો $C_{2}$ ............તરીકે વ્યક્ત કરી શકાય છેView Solution
- 98$'x'.$ પદાર્થ માં $10$ ગ્રામ $6.023 \times 10^{22}$ અણુઑ હાજર છે $ 2 $ લિટર દ્રાવણ માં $5$ ગ્રામ પદાર્થધરાવતાં દ્રાવણ માં સ્થિરતા છે, દ્રાવણ છે ..........$\times 10^{-3}$View Solution
- 99જ્યારે $2.8\, kg$ ડાયનાઇટ્રોજનની માત્રા $1\, kg$ ડાયહાઇડ્રોજન સાથે પ્રક્રિયા આપે છે ત્યારે ઉત્પન્ન થતું એમોનિયાનું દળ............View Solution
- 100$0.1\, N$ $NaOH$ ના ફોસ્ફિનિક એસિડની તટસ્થતા માટે જરૂરી $0.1\, N$નું $10\, mL$ કદ ($ ml $ માં) ........View Solution