Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1પ્રકાશની સૌથી લાંબી તરંગલંબાઈ કે જેનો ઉપયોગ લિથિયમ પરમાણુ $(Li)$ ને તેની ધરા અવસ્થામાંથી આયનીકરણ કરવા માટે થાય છે તે $x \times 10^{-8}\,m$ છે. તો $x$ નું મૂલ્ય છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : હાઈડ્રોજન પરમાણુના પ્રથમ કક્ષામાં (કોશમાં) ઈલેક્ટ્રોનની ઉર્જા $-2.2 \times 10^{-18}\,J ; h =6.63 \times 10^{-34}\,Js$ અને $c =3 \times 10^{8}\,ms ^{-1}$ )
- 2હાઈડ્રોજન પરમાણુની $3^{rd}$ બોહર કક્ષાની ત્રિજ્યા જો $r_3$ હોય અને $4^{th}$ બોહર કક્ષાની ત્રિજ્યા $r_4$હોય તો પછી ....View Solution
- 3$4d$ કક્ષકમાં ત્રિજ્યાકીય અને કોણીય નોડની સંખ્યા અનુક્રમે$\dots\dots$View Solution
- 4ક્યા આયનોના યુગ્મ (જોડી) એ $Al ^{3+}$ સાથે સમઇલેક્ટ્રોનીય છે?View Solution
- 5પ્લેટિનમ ધાતુ સાથે ફોટોઈલેકિટ્રિક અસરને ઉત્પજ્ન કરવાના ક્રમમાં ફોટોન ઓછામાં આછી $\dots\dots\dots$ $....\,\times 10^{-19} \,J$ ઊર્જા ધરાવતી હોવી જરૂરી છે.View Solution
[આપેલ:પ્લેટીનમની દેહલી આવૃત્તિ $1.3$ $\times 10^{15} \,s ^{-1}$ અને $h =6.6 \times 10^{-34} \,J \,s$.]
- 6$2 a _{ o }$ ( જ્યાં $a _{ o }=$ બોહરની ત્રિજ્યા $52.9 \,pm$ ) લંબાઈના એકપરીમાણીય વિસ્તારમાં એક ઈલેક્ટ્રોનના ગતિમાં ન્યૂનતમ અનિશ્ચિતતા $.......\,km\, s ^{-1}$ થશે.View Solution
(આપેલું છે : ઈલેકટ્રોનનું દળ $=9.1 \times 10^{-31} \,kg$, પ્લાન્ક અચળાંક $h =6.63 \times 10^{-34}\, Js$ )
- 7આપેલો પૈકી કયાં જોડકાં સમઈલેકટ્રોનીય સ્પીસીઝોના નથી ?View Solution
(પરમાણુ ક્રમાંક $Sm , 62 ; Er , 68: Yb , 70: Lu , 71 ; Eu , 63: Tb$, $65$; $\operatorname{Tm}, 69)$
- 8જો અવકાશમાં સૂક્ષ્મ કણનો વેગ અને સ્થિતિમાં અનિશ્ચિતા અનુક્રમે $2.4 \times 10^{-26}\left( m s ^{-1}\right)$ અને $10^{-7}( m )$ હોય તો આ કણનું વજન $g$ (ગ્રામ માં).........છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલુ છે : $h =6.626 \times 10^{-34} \,Js$ )
- 9જો હાઈડ્રોજન પરમાણુમાંથી ઉત્સર્જીત એક ઈલેકટ્રોનની તરંગ લંબાઈ $3.3 \times 10^{-10}\,m$ હોય તો, પછી ભૂમિગત અવસ્થામાં ઈલેકટ્રોન વડે શોષિત ઉર્જાની સરખામણીમાં પરમાણુમાંથી છટકવા માટે જરૂરી ન્યૂનત્તમ ઉર્જા $.....$ ગણી છે. (નજીકના પૂર્ણાંકમાં)View Solution
[આપેલું છે $: h =6.626 \times 10^{-34}\,Js$, ઇલેકટ્રોનનું દળ $=9.1 \times 10^{-31}$ ]
- 10નીચે આપેલા વિધાનોને ધ્યાનમાં લો :View Solution
$(A)$ મુખ્ય ક્વોન્ટમ આંક એ '$n' =\,1,2,3, \ldots$ ના મૂલ્યો સાથે ધન પૂર્ણાંક છે.
$(B)$ આપેલ ' $n$ ' (મુખ્ય ક્વોન્ટમ આંક) માટે ગૌણ ક્વોન્ટમ આંક ' $l$ ' એ ' $l$ ' $=0,1,2, \ldots . n$ તરીકેના મૂલ્યો ધરાવે છે.
$(C)$ એક ચૌક્કસ ' $l$ ' માટે (ગૌણ ક્વોન્ટમ આંક) ચુંબકીય કક્ષકીય ક્વોન્ટમ આંક ' $m _{l}$ ' એ $(2 l+1)$ મૂલ્યો ધરાવે છે.
$(D)$ ઈલેક્ટ્રોન સ્પીનના બે શક્ય નિર્દેશન $\pm 1 / 2$ છે.
$(E)\,l=5$ માટે , કુલ $9$ કક્ષકો બનશે.
નીચે આપેલા વિકલ્પોમાંથી સાચું જવાબ પસંદ કરો.
- 11$n =5, m _{l}=+2$ સાથે કક્ષકોની સંખ્યા ...... છે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઓફ કરો)View Solution
- 12${Zn}^{+}$ આયનમાં બાહ્યતમ ઇલેક્ટ્રોનની ચુંબકીય ક્વોન્ટમ આંકનું મૂલ્ય $.....$ છે.View Solution
- 13અનુક્રમે પરમાણુ ક્રમાંકો $33, 53$ અને $83$ ધરાવતાં $X, Y$ અને $Z$ તત્વોની લાક્ષણિકતાઓ શોધો.View Solution
- 14એક $50$ વોટનો બલ્બ $795\, {~nm}$ની તરંગલંબાઇનો મોનોક્રોમેટિક લાલ પ્રકાશ બહાર ફેંકે છે. બલ્બ દ્વારા પ્રતિ સેકન્ડ ઉત્સર્જિત ફોટોનની સંખ્યા ${x} \times 10^{20}$ છે. ${x}$નું મૂલ્ય $......$ છે.View Solution
$\left[\right.$ આપેલ છે $: {h}=6.63 \times 10^{-34} \,{Js}$ અને $\left.{c}=3.0 \times 10^{8} \,{~ms}^{-1}\right]$
- 15એક મોનોક્રોમેટિક (સિંગલ આવૃતી) ઇન્ફ્રારેડ રેન્જ પાવર દ્વારા $1\, {~mW}$ અને તરંગલંબાઇ $1000 \,{~nm}$, $0.1$ સેકન્ડમાં ${x}\, \times 10^{13}$ ઉત્સર્જિત ફોટોનની સંખ્યા છે. ${x}$નું મૂલ્ય $.....$ છે. (નજીકનું પૂર્ણાંક)View Solution
$\left({h}=6.63 \times 10^{-34}\, {Js}, {c}=3.00 \times 10^{8} \,{~ms}^{-1}\right)$
- 16ચોક્કસ ભ્રમણકક્ષા $n =4$ અને $m _{ L }=-3$ ધરાવે છે. આ કક્ષાના રેડિયલ નોડની સંખ્યા .......... છે ?View Solution
- 17View Solutionચોક્કસ ભ્રમણકક્ષામાં કોણીય નોડ્સ અને બે રેડિયલ નોડ્સ નથી,તો તે ભ્રમણકક્ષા કઈ છે?
- 18View Solutionજો અણુનો થોમસન મોડેલ સાચું હોત, તો પછી રુથરફોર્ડના સોનાના વરખ પ્રયોગનું પરિણામ આવત:
- 19ધાતુ $A$ નાં પરમાણનું આયનીકરણ કરવા માટે $663\, nm$ તરંગલંબાઈ વાળા વિદ્યુતચુંબકીય વિકિરણ પર્યાપ્ત છે. તો ધાતુ $A$ ની આયનીકરણ ઊર્જા $kJ\, mol ^{-1}$ માં ..... છે.View Solution
(નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઑફ કરો) $\left[ h =6.63 \times 10^{-34}\, Js , c =3.00 \times 10^{8} \,ms ^{-1}\right.$ $,$ $\left. N _{ A }=6.02 \times 10^{23}\, mol ^{-1}\right]$
- 20ધાતુની સપાટી $500\, {~nm}$ કિરણોત્સર્ગના સંપર્કમાં આવે છે. ફોટોઇલેક્ટ્રિક પ્રવાહ માટે ધાતુની થ્રેશોલ્ડ આવૃતી $4.3 \times 10^{14}\, {~Hz}$ છે. બહાર કાઢેલા ઇલેક્ટ્રોનનો વેગ $.......\,\times 10^{5} {~ms}^{-1}$ (નજીકના પૂર્ણાંકમાં) છે.View Solution
[ઉપયોગ: $\left.{h}=6.63 \times 10^{-34}\, {Js}, {m}_{{e}}=9.0 \times 10^{-31}\, {~kg}\right]$
- 21નીચે બે નિવેદનો આપવામાં આવ્યા છેView Solution
વિધાન $I:$ બોહરના અણુના મોડેલ મુજબ, ન્યુક્લિયસ પરના ધન વિજભારના ઘટાડા સાથે ગુણાત્મક રીતે ઇલેક્ટ્રોનનો વેગ વધે છે કારણ કે ન્યુક્લિયસ દ્વારા ઇલેક્ટ્રોન પર કોઈ મજબૂત બંધન નથી.
વિધાન $II:$ બોહરના અણુના મોડેલ મુજબ, ગુણાત્મક રીતે ઇલેક્ટ્રોનના વેગનું મુલ્ય મુખ્ય ક્વોન્ટમ સંખ્યામાં ઘટાડો સાથે વધે છે.
પ્રકાશમાં ઉપરોક્ત વિધાનોના , નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 22નીચે બે વિધાનો આપેલા છેView Solution
વિધાન $I :$ બોહરનો સિદ્ધાંત $Li ^{+}$ આયનની સ્થિરતા અને લાઇન સ્પેક્ટ્રમ માટે છે.
વિધાન $II :$ બોહરનો સિદ્ધાંત ચુંબકીય ક્ષેત્રની હાજરીમાં વર્ણપટ્ટી રેખાઓનું વિભાજન સમજાવવામાં અસમર્થ હતું.
ઉપરોક્ત વિધાનોના પ્ચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો:
- 23નીચે બે વિધાનો આપ્યા છે:View Solution
વિધાન $I :$ રુથરફોર્ડનો સોનાના વરખનો પ્રયોગ હાઇડ્રોજન અણુના રેખા વર્ણપટને સમજાવી શકતો નથી.
વિધાન $II :$ હાઇડ્રોજન અણુનું બોહર મોડેલ હાઇઝનબર્ગના અનિશ્ચિતતાના સિદ્ધાંતનો વિરોધાભાસ કરે છે.
પ્રકાશમાં ઉપરોક્ત વિધાનોના , નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો:
- 24સમાન પોટેન્શિયલ વડે એક પ્રોટોન અને $Li ^{3+}$ ન્યુક્લિયસ પ્રવેગિત (accelerated) થાય છે. $Li ^{3+}$ અને પ્રોટોનની દ-બ્રોગ્લી તરંગલંબાઈ અનુક્રમે $\lambda_{ Li }$ અને $\lambda_{ p }$ તે હોય તો, $\frac{\lambda_{ Li }}{\lambda_{ p }}$ નું મૂલ્ય $x \times 10^{-1}$ છે. તો $x$ નું મૂલ્ય ........ છે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઑફ) $\left[ Li ^{3+}\right.$ નું દળ $=8.3$ પ્રોટોનનું દળ.]View Solution
- 25હાઇડ્રોજન અણુની બીજી બોહર ભ્રમણકક્ષામાં ઇલેક્ટ્રોનની ગતિ ઊર્જા $\frac{{h}^{2}}{{xma}_{0}^{2}}$ બરાબર છે. $10 {x}$નું મૂલ્ય $....$ છે. $\left({a}_{0}\right.$ બોહરની ભ્રમણકક્ષાની ત્રિજ્યા છે) (નજીકના પૂર્ણાંકમાં) [આપેલ છે : $\pi=3.14]$View Solution
- 26View Solutionબે રેડિયલ તેમજ બે કોણીય નોડ ધરાવતી કક્ષક શોધો.
- 27બોહરનાં પરમાણ્વીય વાદ પ્રમાણે :View Solution
$(A)$ ઈલેક્ટ્રોનની ગતિકીય ઊર્જા $\propto \frac{ Z ^{2}}{ n ^{2}}$
$(B)$ ઈલેક્ટ્રોનનાં વેગ $(v)$ નો અને મુખ્ય ક્વોન્ટમ આંક $(n)$ નો ગુણાંક (product) $'vn'$ $\propto Z ^{2}.$
$(C)$ કક્ષામાં ઈલેક્ટ્રૉન નાં પરિભ્રમણ (revolution) ની આવૃત્તિ $\propto \frac{ Z ^{3}}{ n ^{3}}$
$(D)$ ઈલેક્ટ્રૉન ઉપર લાગતા આકર્ષણનાં કુલંબિક બળો $\propto \frac{ Z ^{3}}{ n ^{4}}$
નીચે દર્શાવેલ વિકલ્પોમાંથી સૌથી વધુ બંધબેસતો જવાબ પસંદ કરો.
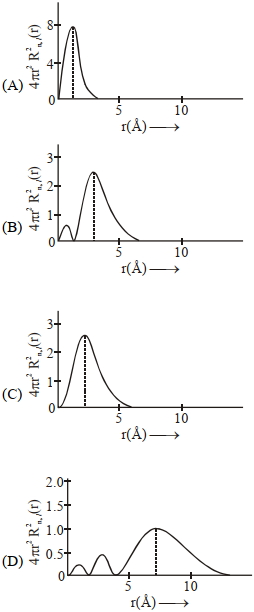
- 28હાઈડ્રોજન પરમાણુની વિવિધ કક્ષકો માટે ત્રિજ્યા વિતરણ વિધેય વિરુદ્ધ $'r'$ ના આલેખ નીચે આપેલ છેView Solution
${image}$
તો, $3s$ કક્ષક માટે સાચો આલેખ શોધો
- 29$400\, {~nm}$ તરંગલંબાઇના મોનોક્રોમેટિક કિરણોત્સર્ગનો સ્રોત $1000\, {~J}$ ઊર્જા $10$ સેકન્ડમાં પૂરી પાડે છે. જ્યારે આ કિરણોત્સર્ગ સોડિયમની સપાટી પર પડે છે, ત્યારે ${x} \times 10^{20}$ ઇલેક્ટ્રોન પ્રતિ સેકન્ડ બહાર કાવામાં આવે છે.ધારો કે તરંગલંબાઇ $400\, {~nm}$ સોડિયમ ધાતુની સપાટીથી ઇલેક્ટ્રોનને બહાર કાવા માટે પૂરતું છે.$x$ નું મૂલ્ય $......$ છે. (નજીકનાં પૂર્ણાંકમાં) $\left({h}=6.626 \times 10^{-34}\, {Js}\right)$View Solution
- 30ઇલેક્ટ્રોનની તરંગલંબાઇ $40\, {kV}$ના પોટેન્શિયલ તફાવત દ્વારા ${X}\, \times$ $10^{-12} \,{~m}$ સ્થિર અવસ્થાથી વેગ આપે છે.${x}$નું મૂલ્ય $.....$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
આપેલ છે: ઇલેક્ટ્રોનનું દળ $=9.1 \times 10^{-31}\, {~kg}$
ઇલેક્ટ્રોનનો વીજભાર $=1.6 \times 10^{-19}\, {C}$
પ્લાન્ક અચળાંક $=6.63 \times 10^{-34\,} {Js}$
- 31જ્યારે પ્રકાશની તરંગલંબાઇ $248\, nm$ ધાતુની થ્રેશોલ્ડ ઊર્જા $3.0 \,eV$ પર પડે છે,ત્યારે ઉત્સર્જિત ઇલેક્ટ્રોનની દ-બ્રોગ્લીની તરંગલંબાઇ ............ $\mathring A$View Solution
[ઉપયોગ કરો : $\sqrt{3}=1.73, h =6.63 \times 10^{-34} Js$ $m _{ e }=9.1 \times 10^{-31} kg ; c =3.0 \times 10^{8} ms ^{-1}$ $\left.1 eV =1.6 \times 10^{-19} J \right]$
- 32પ્રવેગિત ઇલેક્ટ્રોન $0.02\,\%$ની અનિશ્ચિતતા સાથે $5 \times 10^{6} \,{~ms}^{-1}$ની ઝડપ ધરાવે છે. ગતિમાં હોય ત્યારે તેનું સ્થાન શોધવામાં અનિશ્ચિતતા $x \times 10^{-9}\, {~m}$ છે. $x$ નું મૂલ્ય $......$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
[ઇલેક્ટ્રોનનું દળ $\left.=9.1 \times 10^{-31}\, {~kg}, {~h}=6.63 \times 10^{-34}\, {~J} {~s}, \pi=3.14\right]$
- 33$n=5,\;m_s=+\frac 12$ ક્વોન્ટમ સંખ્યા સાથે સંકળાયેલ ભ્રમણકક્ષાની સંખ્યા ........ થાય.View Solution
- 34View Solutionકઈ આકૃતિ જે અણુઓની ક્વોન્ટમ પ્રકૃતિનો સીધો અભિવ્યક્તિ નથી
- 35View Solutionછઠ્ઠી હરોળમાં, કક્ષા કઈ રીતે ભરાઈ છે?
- 36$n=4$ અને $m =-2$ ક્વોન્ટમ આંક સાથે સંકળાયેલ પેટા કક્ષકની સંખ્યા કેટલી છે:View Solution
- 37View Solutionવિદ્યુતચુંબકીય વર્ણપટનો કયો વિસ્તાર જ્યાં બાલ્મર શ્રેણીની રેખાઓ દેખાય છે?
- 38$Li ^{2+}$ ની $3^{\text {rd }}$ અને $4^{\text {th }}$ કક્ષક વચ્ચેનો તફાવત $\Delta R _{1}$ છે. $He ^{+}$ ની $3^{\text {rd }}$ અને $4^{\text {th }}$ કક્ષક વચ્ચેનો તફાવત $\Delta R _{2}$ છે.$\Delta R _{1}: \Delta R _{2}$નો ગુણોતર :View Solution
- 39$\mathrm{H}$ પરમાણુના સ્પેક્ટ્રમ માં બામર શ્રેણી માટે , $\quad \bar{v}=R_{H}\left\{\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right\}, \quad$ નીચેના પૈકી કયા વિધાનો સાચા છે,View Solution
$(I)$ જેમ જેમ તરંગલંબાઈ ઘટે છે, તેમ શ્રેણીની રેખાઓ એક બીજામાં ભળી જાય છે
$(II)$ પૂર્ણાંક $n_{1}$ એ $2$ બરાબર થાય છે.
$(III)$ સૌથી લાંબી તરંગલંબાઇની રેખાઓ અનુરૂપ $\mathrm{n}_{2}=3$ છે .
$(IV)$ હાઇડ્રોજનની આયનીકરણ ઊર્જા આ રેખાઓની તરંગ સંખ્યામાંથી ગણતરી કરી શકાય છે
- 40લાયમન શ્રેણીમાં $H$ પરમાણુની ટૂંકી તરંગલંબાઇ એ $\lambda_{1}$ છે.$He ^{+}$ની બાલ્મર શ્રેણીની સૌથી લાંબી તરંગલંબાઇ કઈ છે:View Solution
- 41કાલ્પનિક પરિસ્થિતિને ધ્યાનમાં લો જ્યાં ગૌણ ક્વોન્ટમ આંક $l$$0$ , $1,2, \ldots \ldots n+1,$ ની કિંમતો લે છે જ્યાં $n$ એ મુખ્ય ક્વોન્ટમ આંક છે ત્યારે અણુ સંખ્યા સાથેનું તત્વView Solution
- 42$4^{th}$ બોહર ભ્રમણકક્ષા ની ઇલેક્ટ્રોનની દ બ્રોગ્લી તરંગલંબાઇ .......... થાય .View Solution
- 43${\left| \psi \right|^2}$ અને $r$(radial distance) વચ્ચેનો આલેખ નીચે દર્શાવ્યો છે . તે .. . રજૂ કરે છે .View Solution
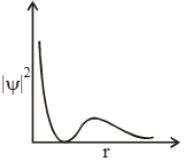
- 44View Solutionઇલેક્ટ્રોન મળવાની વધુ સંભાવના . . . માં છે .
- 45View Solutionનીચેના પૈકી શામાં 2s કક્ષકની ઊર્જા સૌથી ઓછી છે ?
- 46પરમાણ્વીય હાઈડ્રોજનના વર્ણપટ રેખાઓની કોઈ આપેલી શ્રેણી માટે $\Delta \bar V\, = \,\Delta {\bar V_{\max }}\, - \,\Delta {\bar V_{\min }}$ એ $cm^{-1}$ માં મહતમ અને ન્યૂનતમ આવૃતિઓનો તફાવત છે . $\Delta {\bar V_{Lymann}}/\,\Delta {\bar V_{Balmer}}$ ગુણોતર જણાવો.View Solution
- 47સ્નાયુની દુખાવાની ઉષ્મા સારવાર આશરે $900\,nm$ તરંગલંબાઈના વિકિરણનો સમાવેશ કરે છે. આ હેતુ માટે $H -$ પરમાણુની કઈ વર્ણપટ રેખા યોગ્ય છેView Solution
$[{R_H} = 1 \times {10^5}\,c{m^{ - 1}},\,h\, = 6.6\, \times {10^{ - 34}}\,Js\,\,c = 3\, \times \,{10^8}\,m{s^{ - 1}}]$
- 48હાઈડ્રોજન પરમાણુની ધરા અવસ્થાની ઊર્જા $-13.6\, eV$ છે તો $He^+$ આયનની દ્રીતીય ઉતેજિત અવસ્થા ( $eV$ માં ) કેટલી થાય?View Solution
- 49હાઈડ્રોજન વર્ણપટની બે વર્ણપટ શ્રેણીઓની સૌથી ટૂંકી તરંગ લંબાઈઓનો ગુણોતર $9$ છે . તો વર્ણપટ શ્રેણીઓ જણાવો.View Solution
- 50ચાર ઇલેક્ટ્રોન ના કવોન્ટમ આંક નીચે આપેલ છે.View Solution
$I. n = 4,l = 2,m_l = -2, m_s = -1/ 2$
$II. n = 3,l = 2, m_l = 1,m_s = +1/ 2$
$III. n = 4,l = 1, m_l = 0, m_s = +1/ 2$
$IV. n = 3,l = 1, m_l = 1; m_s = -1/ 2$
તેઓની વધતી ઊર્જાનો સાચો ક્રમ જણાવો. - 51જો $4000\, \mathop A\limits^o $ તરંગલંબાઈનો પ્રકાશ ધાતુમાંથી $6\times10^5\, ms^{-1}$ વેગ ધરાવતા ફોટોઇલેક્ટ્રોનનું ઉત્સર્જન કરે તો ધાતુનું કાર્યવિધેય ............... $\mathrm{eV}$ થશે ?View Solution
( ઇલેક્ટ્રોનનું દળ $= 9\times10^{-31}\, kg$ પ્રકાશનો વેગ $= 3\times10^8\, ms^{-1}$ પ્લાન્ક અચળાંક $= 6.626\times10^{-34}\, Js$ ઇલેક્ટ્રોનનો વીજભાર $= 1.6\times10^{-19}\, J\,eV^{-1}$)
- 52જો $\lambda $ તરંગલંબાઈના પ્રકાશને ધાતુની સપાટી પર વિકિરીત કરવાથી મુક્ત થતાં સૌથી ઝડપી ઇલેક્ટ્રોનનું વેગમાન $p$ હોયતો ફોટોઇલેક્ટ્રોનનું વેગમાન $p$ હોય તો ફોટો ઇલેક્ટ્રોનનું વેગમાન $1.5\, p$ હોવા માટે પ્રકાશની તરંગલંબાઈ શું હોવી જોઇયે ?View Solution
(મુક્ત થતાં ઇલેક્ટ્રોનની ગતિ ઊર્જા તેના કાર્યવિધેયની સરખામણી ઘણી વધારે હોવાનું ધારો )
- 53પરમાણ્વીય કક્ષકોના અર્થઘટનના સંદર્ભમાં નીચેના પૈકી ક્યાં વિધાનોનું સંયુગ્મન સાચું છે.View Solution
$(1)$ નીચું કોણીય વેગમાન ધરાવતી કક્ષકમાના ઇલેક્ટ્રોન કરતાં ઊંચું કોણીય વેગમાન ધરાવતી કક્ષકોમાનો ઇલેક્ટ્રોન કેન્દ્રથી દૂર રહે છે .
$(2)$ મુખ્ય ક્વોન્ટમ આંકના આપેલા મૂલ્ય માટે, કક્ષકનું કદ ગૌણ ક્વોન્ટમ આંકના વ્યસ્ત પ્રમાણમાં હોય છે .
$(3)$ તરંગ યંત્રશાસ્ત્ર અનુસાર , ધરા અવસ્થાનું કોણીય વેગમાન $\frac {h}{2\pi }$ બરાબર હોય છે .
$(4)$ વિવિધ ગૌણ ક્વોન્ટમ આંક માટે $\Psi \,\,Vs\,\,r$ નો આલેખ, ઊંચા $r$ મૂલ્ય તરફ શિખરનું સ્થાનાંતર દર્શાવે છે .
- 54ફોટોઇલેક્ટ્રોન સાથે સંકળાયેલી દ-બ્રોગ્લી તરંગ લંબાઈ $\left( \lambda \right)$ એ આપાત પ્રકાશની આવ્રુતિ $(v)$ સાથે કઈ રીતે ચાલે છે ? [$v_0$ એ દેહલિજ આવ્રુતિ છે ]:View Solution
- 55View Solutionસમઇલેક્ટ્રોનીય આયનોનો સેટ જણાવો.
- 56હાઈડ્રોજન $(hydrogenic )$ જેવા પરમાણુમાં બોહરની $n^{th}$ ક્ક્ષામાં ઇલેક્ટ્રોનની દ-બ્રોગ્લી તરંગ લંબાઈ $1.5\,\pi a_0$ ( $a_0$ બોહરની ત્રિજ્યા છે ), તો $n/z$ નું મૂલ્ય કેટલું થશે?View Solution
- 57હોઈડ્રોજન પરમાણુની $1\,s$ કક્ષકમાં રહેલા ઇલેક્ટ્રોન અંગે નીચેના પૈકી ક્યૂ વિધાન ખોટું છે ? ( બોહરની ત્રિજ્યા $a_0$ વડે રજૂ કરવામાં આવે છે . )View Solution
- 58$n_i= 8$ માંથી $n_f $ માં પરમાણ્વિય હાઈડ્રોજન ઉત્સર્જન રેખા માટે તરંગલંબાઈ $\left( {\bar v} \right)$ વિરુદ્ધ $\left( {\frac{1}{{{n^2}}}} \right)$ નો આલેખ શું થશે ? (રીડબર્ગ અચળાંક $R_H$ એ તરંગઆંકના એકમમા છે )View Solution
- 59View Solutionનીચેના પૈકી ક્યુ વિધાન ખોટુ છે ?
- 60$'H'$ પરમાણુની બોહરની પ્રથમ કક્ષમાં હાજર ઇલેક્ટ્રોનની દ-બ્રોગ્લી તરંગલંબાઈ જણાવો.View Solution
- 61ફોટોઇલેક્ટ્રિક અસરના પ્રયોગમાં જ્યારે $250\, nm$ ના વિકિરણનો ઉપયોગ કરવામાં આવે ત્યારે ધાતુમાંથી ફોટો ઇલેક્ટ્રોનનું ઉત્સર્જન $0.5\,V$ લાગુ પાડીને અટકાવી શકાય છે. તો ધાતુનું કાર્યવિધેય ............... $\mathrm{eV}$ જણાવો.View Solution
- 62તંદુરસ્ત પુખ્ત વયના માનવ શરીરમાં સમૂહ દ્વારા સૌથી વધુ વિપુલ તત્વો : ઓક્સિજન $(61.4\%);$ કાર્બન $(22.9\%),$ હાઈડ્રોજન $(10.0\%);$ અને નાઈટ્રોજન $(2.6\%).$View Solution
જો $75$કિલોગ્રામ વજન ધરાવતી વ્યક્તિ જો બધા $^1H$ પરમાણુઓ $^2H$ અણુઓ દ્વારા બદલવામાં આવે તો તે ....... કિગ્રા છે.
- 63હાઈડ્રોજન પરમાણુમાં એક ઇલેક્ટ્રોન ઊંચી કક્ષકમાંથી $211.6\,pm$ ત્રિજ્યાની કક્ષકમાં સંક્રાંતિ અનુભવે છે. આ સંક્રાતિ કોની સાથે સંકળાયેલ છે ?View Solution
- 64હાઈડ્રોજન પરમાણુ માટે બોહરની દ્વિતીય કક્ષાની ત્રિજ્યા .......... $\mathop A\limits^o $.View Solution
(પ્લાંક અચળાંક $ h = 6. \times 10^{-34}\, Js\,;$ ઇલેક્ટ્રોનનું દળ $= 9.1091 \times 10^{-31}\, kg\,;$ ઇલેક્ટ્રોનનો વિજભાર $e= 1.60210 \times 10^{-19}\, C\,;$ શૂન્યાવકાશની પારગમ્યતા $\epsilon _0 = 8.854185 \times 10^{-12} \,kg^{-1} \,m^{-3} A^2$)
- 65જો હાઈડ્રોજન પરમાણુની લાયમેન શ્રેણીની સૌથી ટૂંકી તરંગલંબાઈ $A$ હોય તો $He^+$ ની પાશ્વન શ્રેણીની સૌથી લાંબી તરંગલંબાઈ જણાવો.View Solution
- 66એક ગરમ કરેલા ફિલામેન્ટમાંથી નીકળતા ઇલેક્ટ્રોનના પ્રવાહીને $V \,esu$ જેટલા તફાવતે રાખેલા બે વિજભારિત પ્લેટો વચ્ચેથી પસાર કરવામાં આવે છે. જો $e$ અને $m$ ઇલેક્ટ્રોનના અનુક્રમે વિજભાર અને દળ હોય તો $h/ \lambda$ નુ મૂલ્ય ............ દ્વારા આપવામાં આવે છે.View Solution
($\lambda$ એ ઇલેક્ટ્રોનના તરંગ સાથે સંકળાયેલી તરંગલંબાઈ છે)
- 67મુખ્ય ક્વોન્ટમ આંક $5$ સાથે સંકળાયેલ કક્ષકોની કુલ સંખ્યા જણાવો.View Solution
- 68$T$ તાપમાને કોય પણ કણની સરેરાશ ગતિઊર્જા $\frac{3}{2}\,kT$ છે. તો દ-બ્રોગ્લી તરંગલંબાઈ ક્યા ક્રમને અનુસરશે ?View Solution
- 69જો મુખ્ય ક્વોન્ટમ આંક $n = 6$ હોય તો ઇલેક્ટ્રોનની ગોઠવણીનો સાચો ક્રમ જણાવો.View Solution
- 70નીચે આપેલી ઉર્જાઓ પૈકી .............. $\mathrm{eV}$ એક હાઈડ્રોજનની સંભવિત ઉતેજિત અવસ્થાની ઊર્જા છે ?View Solution
- 71$100\,ms^{-1}$ ના વેગથી ગતિ કરતા $6.63\,g$ દળની કણની દ-બ્રોગ્લી તરંગલંબાઈ જણાવો.View Solution
- 72$\Delta E = - 2.0 \times {10^{ - 18}}\,J\left( {\frac{1}{{n_2^2}} - \frac{1}{{n_1^2}}} \right)$ સમીકરણને આધારે હાઈડ્રોજન ઇલેક્ટ્રોનને $n = 1$ સ્તરમાંથી $n = 2$ સ્તરમાં ઉતેજિત કરવા શોષણ પામતા પ્રકાશની તરંગલંબાઈ જણાવો.View Solution
$(h\, = 6.625\times10^{-34}\, J\,s,\, c\, = 3\times10^8\, m\,s^{-1})$
- 73ઉતેજિત હાઈડ્રોજન પરમાણુ $2.47 \times 10^{15}\,Hz.$ પર પારજાંબલી વિસ્તારમાં પ્રકાશનુ ઉત્સર્જન કરે છે . તો આવૃતિ સાથેના એક ફોટોનની ઊર્જા શું થશે ?View Solution
$(h = 6.63 \times 10^{-34}\,Js)$
- 74જો $\lambda_0$ અને $\lambda$ અનુક્રમે દેહલીજ તરંગલંબાઈ આપાત પ્રકાશની તરંગલંબાઈ હોય તો ધાતુની સપાટી પરથી મુક્ત થતા ફોટોઇલેક્ટ્રોનનો વેગ જણાવો.View Solution
- 75જો $m$ અને $e$ એ હાઈડ્રોજન પરમાણુ માટે $r$ ત્રિજ્યાની ક્ક્ષામાં ફરતા ઇલેક્ટ્રોનના દળ અને વીજભાર હોય તો ફરતા ઇલેક્ટ્રોનની કુલ ઊર્જા શુ થશે ?View Solution
- 76વાયુરૂપ $Na$ પરમાણુઓની આયનીકરણ ઊર્જા $495.5\, kJ\, mol^{-1}$ છે. તો સોડિયમ પરમાણુની આયનીકરણ કરતા પ્રકાશની સૌથી ઓછી શક્ય આવૃતિ જણાવો .View Solution
$(h\, = 6.626 \times 10^{-34}\, Js, N_A\, = 6.022 \times 10^{23}\, mol^{-1} )$
- 77$1000\, kg$ દળની અને $36\, km/hr$ ના વેગની ગતિ કરતી કારની દ-બ્રોગ્લી તરંગ લંબાઈ જણાવો.View Solution
- 78$(A)\, n = 5, m_l= + 1$ $(B)\, n =2, l =1, m_l= -1, m_s = -1/2$ આપેલ છે . તો $(A)$ અને $(B)$ માં આપેલ ક્વોન્ટમ આંક મુજબ પરમાણુમા ઇલેક્ટ્રોનની મહતમ સંખ્યા અનુક્રમે જણાવોView Solution
- 79કોઈ એક પરમાણુમા કેટલી કક્ષકો, ક્વોન્ટમ આંક $n = 3, l = 2$ અને $m_l = + 2$ ધરાવે છે ?View Solution
- 80હાઈડ્રોજન વર્ણપટની બામર શ્રેણીમા પ્રથમ ઉત્સર્જન રેખાનો તરંગ આંક જણાવો. $(\,R =$ રીડબર્ગ અચળાંક $)$View Solution
- 81એકઇલેક્ટ્રોનની ઊર્જા નીચે પ્રમાણે દર્શાવેલ છે.View Solution
$E =- 2.178 \times 10^{-18}\,J \, \left( {\frac{{{Z^2}}}{{{n^2}}}} \right)$ તો હાઈડ્રોજન પરમાણુમાં રહેલા ઇલેક્ટ્રોનને $n = 1$ થી $n = 2$ શક્તિસ્તરમાં ઉતેજિત કરવા માટે કેટલી તરંગલંબાઈ પ્રકાશની જરૂર પડશે ?
$(h = 6.62 \times 10^{-34} \,J\,s , c = 3.0 \times 10^8 \,ms^{-1})$
- 82$3s$ અને $2p$ કક્ષકના રેડિયલ (અરિય) નોડ્સની સંખ્યા અનુક્રમે શું છે ?View Solution
- 83View Solutionનીચેનામાંથી કઈ કક્ષકની ત્રિજ્યા હાઇડ્રોજન અણુના પ્રથમ બોહરની કક્ષકની સમાન છે?
- 84નીચેનામાંથી ક્યા સમઇલેક્ટ્રોનિક અને સમબંધારણીય છે $NO_3^ - ,\,CO_3^{2 - },\,ClO_3^ - ,\,S{O_3}$View Solution
- 85નીચે પૈકી કોણ સમઇલેક્ટ્રોનિય અને સમબંધારણીય $NO_3^ - ,\,CO_3^{2 - },\,ClO_3^ - ,\,S{O_3}$ છે?View Solution
- 86ઇલેક્ટ્રોન સ્પિન માટેના ક્વોન્ટમ નંબર્સ $+ 1/2$ અને $-1/2$ શું રજૂ કરે છે ?View Solution
- 87ઇલેક્ટ્રોન સ્પિન માટેના ક્વોન્ટમ નંબર્સ $+1/2$ અને $-1/2$ શું રજૂ કરે છે ?View Solution
- 88${p_x}$ માં નોડલ સમતલની સંખ્યા કેટલી છે ?View Solution
- 89એક તત્વ ની ઇલેક્ટ્રોનિય રચના $1{s^2}2{s^2}2{p^6}3{s^2}3{p^6}3{d^5}4{s^1}$ છે. તે શુ દર્શાવે છે ?View Solution
- 90ક્વોન્ટમ નંબર $n$ અને $l$ $(i)$ $n = 4,\,l = 1$ $(ii)$ $n = 4,\,l = 0$ $(iii)$ $n = 3,\,l = 2$ $(iv)$ $n = 3,\,l = 1$ એ ઉર્જાને નીચાથી ઉચ્ચતમમાં વધારવા માટે મૂકી શકાય છે,View Solution
- 91ઇલેક્ટ્રોન, $n$ અને $l,$ સંખ્યા ક્વોન્ટમ દ્વારા ઓળખાય છે $(i)\, n = 4, l= 1$ $(ii)\, n = 4, l = 0$ $(iii)\, n = 3, l = 2$ $(iv)\,n = 3, l = 1$ નીચાથી લઈને ઉચ્ચતમ સુધી, વધતીઉર્જાના કયા ક્રમમાં મૂકી શકાય છેView Solution
- 92View Solutionનાઇટ્રોજન અણુની ધરા અવસ્થા ઇલેક્ટ્રોનિક ગોઠવણી કોના દ્વારા રજૂ કરી શકાય છે ?
- 93$H$ અણુના પ્રથમ બોહર ભ્રમણકક્ષામાં ઇલેક્ટ્રોનની ઉર્જા $ - 13.6\,eV$ છે બોહરની ભ્રમણકક્ષામાં ઇલેક્ટ્રોન માટે સંભવિત $(s)$ ઉર્જા ની શક્ય ઉર્જા મૂલ્ય હાઇડ્રોજનની ભ્રમણકક્ષા છે (છે) ............. $\mathrm{eV}$View Solution
- 94View Solutionનીચેનામાથી કયા વિધાનો સાચા છે ?
- 95View Solutionઅણુના બંધારણને સમજાવવા માટે ક્વોન્ટમ થિયરીનો પ્રથમ ઉપયોગ કોના દ્વારા કરવામાં આવ્યો હતો ?
- 96View Solutionનીચેનામાંથી કયા આયનમાં અયુગ્મિત ઇલેક્ટ્રોનની સંખ્યા સૌથી વધારે છે ?
- 97$3p$ કક્ષક શું હશે ?View Solution
- 98View Solutionક્વોન્ટમ નંબરોના આપેલા સેટમાંથી તે કયા સિદ્ધાંત સાથે અસંગત છે
- 99View Solutionક્રોમિયમ અણુની ધરા અવસ્થા માં યોગ્ય ઇલેક્ટ્રોનિય રચના શું છે ?
- 100નીચેનામાંથી સમઇલેક્ટ્રોનિક બંધારણ પસંદ કરોView Solution
$\mathop {CH_3^ + }\limits_{\rm{I}} $ $\mathop {{H_3}{O^ + }}\limits_{{\rm{II}}} $ $\mathop {N{H_3}}\limits_{{\rm{III}}} $ $\mathop {CH_3^ - }\limits_{{\rm{IV}}} $