Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionનીચેના કયા પરમાણુ સાથે, ઇલેક્ટ્રોનનું જોડાણ સૌથી મુશ્કેલ છે?
- 2View Solutionનીચેના ક્યા આયનની સૌથી નાની ત્રિજ્યા છે?
- 3View Solutionનીચેના તત્વોની આયનીકરણ શક્તિનો ઘટતો ક્રમ કયો હશે?
- 4View Solutionનીચેના તત્વોની વિધુતઋણતાનો વધતો ક્રમ કયો છે?
- 5નીચેના પૈકી આયનીકરણ એન્થાલ્પીનો સાચો ક્રમ ક્યો છે ?View Solution
$(i)$ $Be^+ > Be$ $(ii)$ $Be > Be^+$ $(iii)$ $C > Be$ $(iv)$ $B > Be$
- 6View Solutionનીચેના પૈકી કઇ ઇલેક્ટ્રોન રચના માટે આયનીકરણ એન્થાપી સૌથી વધુ છે ?
- 7View Solutionનીચેના પૈકી કોણ અનુક્રમે સૌથી વધુ અને સૌથી ઓછી ઋણ ઇલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પી ધરાવે છે ?
- 8View Solutionનીચેના પૈકી કોના ઓક્સાઇડ ઉભયગુણી છે ?
- 9View Solutionનીચેના પૈકી કોના ઓક્સાઇડ ઉભયગુણી છે ?
- 10View Solutionનીચેના પૈકી ક્યુ ઇલેક્ટ્રોનીય બંધારણ ધરાવતા પરમાણુની પ્રથમ આયનીકરણ એન્થાલ્પી સૌથી ઓછી હશે ?
- 11View Solutionનીચેના પૈકી ક્યુ વિધાન ખોટુ છે ?
- 12View Solutionનીચેના પૈકી ક્યુ વિધાન ખોટુ છે?
- 13View Solutionનીચેના પૈકી ક્યુ વિધાન સાચું છે ?
- 14View Solutionનીચેના પૈકી ક્યુ વિધાન સાચુ નથી ?
- 15View Solutionનીચેના પૈકી ક્યો ક્રમ ખોટો છે ?
- 16View Solutionનીચેના પૈકી વિધુતઋણતાનો ક્યો ક્રમ સાચો છે ?
- 17View Solutionનીચેના પૈકી શામાં મહત્તમ ઊર્જા મુક્ત થશે ?
- 18View Solutionનીચેનામાંથી કઇ ધાતુમાં સૌથી વધુ ત્રીજી આયનીકરણ એન્થાલ્પી નો સમાવેશ થાય છે?
- 19View Solutionનીચેનામાંથી કઈ જોડીમાં, બંને ઘટકો સમઇલેક્ટ્રોનિય છે પરંતુ પ્રથમ એક બીજા કરતા કદમાં મોટી છે?
- 20View Solutionનીચેનામાંથી કયા આયનની આયનિક ત્રિજ્યા સૌથી વધુ હશે?
- 21View Solutionનીચેનામાંથી કયા આયનોની અસ્તિત્વની સંભાવના છે?
- 22View Solutionનીચેનામાંથી કયા ઈલેક્ટ્રોનિક બંધારણ દ્વારા એક સંયોજક ધન વાયુમય આયન બનાવવાની વૃતિ સૌથી વધુ હશે?
- 23View Solutionનીચેનામાંથી કયા ઘટકમાં સૌથી બાહ્યતમ કોશમાં અને પીન અલ્ટીમેટ કોશ માં ઈલેક્ટ્રોનની સંખ્યા સમાન હોય?
- 24નીચેનામાંથી કયા તત્વની $I{E_1}$ મૂલ્ય સૌથી ઓછું હોય છે?View Solution
- 25View Solutionનીચેનામાંથી કયા પરમાણુની ઉત્તેજિત સ્થિતિનું પ્રતિનિધિત્વ કરે છે?
- 26View Solutionનીચેનામાંથી કયુ જોડી તત્વો સમાન આવર્ત સાથે સંબંધિત છે?
- 27View Solutionનીચેનામાંથી કયું વિધાન ખોટું છે?
- 28View Solutionનીચેનામાંથી કયું વિધાન ખોટું છે?
- 29View Solutionનીચેનામાંથી કયું વિધાન સાચું છે?
- 30View Solutionનીચેનામાંથી કયો તત્વો ધન અને ઋણ ઑક્સિડેશન બંને સ્થિતિ બતાવે છે?
- 31View Solutionનીચેનામાંથી ક્યા તત્ત્વોની જોડનો આવર્તકોષ્ટકમાં પ્રતિનિધિ તત્વોના સમૂહમાં સમાવેશ થશે ?
- 32View Solutionનીચેના માંથી ક્યો પરમાણુ ઓછી સંહસયોજક ત્રિજ્યા ધરાવે છે
- 33View Solutionનીચેનામાંથી તત્ત્વોની કઇ શ્રેણીની પરમાણ્વિય ત્રિજ્યા લગભગ સમાન થશે ?
- 34View Solutionનીચેનામાંથી પરમાણ્વિય / આયનીય ત્રિજ્યાનો ક્યો ક્રમ સાચો નથી ?
- 35View Solutionનીચેના રૂપરેખાંકનોમાં,કયું તત્વ છે કે જેમાં સૌથી વધુ ઇલેક્ટ્રોન આકર્ષણ છે
- 36View Solutionનીચેનીમાંથી કઈ એક જોડી અલગ છે?
- 37View Solutionનીચે પૈકીખોટું વિધાન કયું છે?
- 38View Solution....... ને કારણે સમૂહનુ પ્રથમ તત્વ સમૂહના અન્ય ભારે સભ્યો કરતા ધણી રીતે જુદુ પડે છે.
- 39પરમાણુક્રમાંક $33$ ધરાવતું તત્વ નીચેનામાંથી ક્યા સમૂહનું તત્વ છે?View Solution
- 40View Solutionપરમાણુની ત્રિજ્યા વિશે સાયુ વિધાન પસંદ કરો.
- 41View Solutionપાંચમા આવર્તમાં હાજર તત્વોની સંખ્યા કેટલી છે
- 42પ્રથમ આયનીકરણ એન્થાલ્પીનો સાચો ક્રમ નીચેનામાંથી ક્યો છે ?View Solution
$(i)$ $Li < B < Be < C$ $(ii)$ $O < N < F$ $(iii)$ $Be < N < Ne$
- 43View Solutionબીજી ઇલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પી એ
- 44View Solutionબીજી આયનીકરણ ઉર્જા શેમાં મહત્તમ છે
- 45View Solutionબોરોનની આયનીકરણ ઉર્જા બેરિલિયમ કરતા ઓછી છે કારણ કે
- 46View Solutionવિધુતઋણતાના મૂલ્યોના ઘટતા ક્રમમાં ગોઠવો.
- 47View Solutionવિધુતઋણતાના મૂલ્યોનો સાચો ઘટતો ક્રમ ક્યો છે ?
- 48View Solutionસંક્રાંતિ શ્રેણીની પ્રથમ હરોળના ચાર ક્રમિક તત્વો તેમના પરમાણુક્રમાંક સાથે દર્શાવ્યા છે. તેમાંથી કયા તત્વની ત્રીજી આયનીકરણ શક્તિ સૌથી વધુ અપેક્ષિત છે?
- 49સામાન્ય ઇલેક્ટ્રોનીય બંધારણ $\left( {n - 2} \right){f^{1 - 14}}\left( {n - 1} \right){d^{0 - 1}}\,n{s^2}$ માં જો $n = 7$ હોય તો તે બંધારણ ........ હશે.View Solution
- 50સોડિયમ અને મેગ્નેશિયમની પ્રથમ $(I)$ અને દ્વિતીય $(II)$ આયનીકરણ એન્થાલ્પીના સંબંધ વિશે શુ સાચુ છે ?View Solution
- 51સોડિયમ સામાન્ય રીતે $ + 2$ ની ઑક્સિડેશન સ્થિતિ બતાવતું નથી કારણકેView Solution
- 52View Solutionસૌથી નીચી પ્રથમ આયનીકરણ ઊર્જા કોની છે ?
- 53View Solutionહેલોજનની ઇલેક્ટ્રોન બંધુતાનો સાચો ક્રમ જણાવો
- 54View Solutionહેલોજનની ઇલેક્ટ્રોન બંધુતા માટે નીચેના પૈકી ક્યુ સાચુ છે ?
- 55View Solutionહેલોજન સમૂહમાં નીચે તરફ જતાં નીચેનામાંથી શું ઘટે છે?
- 56View Solutionહેલોજન સમૂહમાં, પાઉલિંગ સ્કેલ પ્રમાણે ફલોરિનની વિધુતઋણતા સૌથી વધુ છે, પરંતુ ફ્લોરિન ઇલેક્ટ્રોન બંધુતા ક્લોરિન કરતા ઓછી છે. કારણ કે ....
- 57$\mathrm{O}^{2-}, \mathrm{F}^{-}, \mathrm{Na}^{+}$અને $\mathrm{Mg}^{2+}$ સ્પીસીઝો ના સંદર્ભમાં વિધાન(નો) કે જે સાચા છે તે શોધો -View Solution
$(A)$ બધા જ સમઈલેક્ટ્રોનીય છે.
$(B)$ બધા જ સમાન(સરખો) ન્યુક્લિયર (કેન્દ્રીય) ભાર ધરાવે છે.
$(C)$ $\mathrm{O}^{2-}$ એ સૌથી વધારે આયનીક ત્રિજ્યા ધરાવે છે.
$(D)$ $\mathrm{Mg}^{2+}$ એ સૌથી ઓછી (નાની) આયનીક ત્રિન્યા ધરાવે છે.
નીચે આપેલા વિકલ્પોમાંથી સૌથી બંધબેસતો જવાબ પસંદ કરો.
- 58$p$-વિભાગના તત્વો અને તેમના સંયોજનોના સંદભમાં સાચા વિધાનો ઓળખી બતાવો.View Solution
($A$) અધાતુઓ, ધાતુઓ કરતા વધારે (અધિક) વિધૃતઋણતા ધરાવે છે.
($B$) અધાતુઓ, ધાતુઓ કરતા ઓછી (નીચી) આયનીકરણ એન્થાલ્યી ધરાવે છે.
($C$) અત્યંત (વધુ) સક્રિય અધાતુઓ અને અત્યંત (વધુ) સદ્રિય ધાતુઓ માંથી બનતા સંયોજનો સામાન્ય રીતે આયનીક હોય છે.
($D$) અધાતુ ના ઓકસાઈડો સામાન્ય રીતે પ્રકૃતિમાં બેજિક હોય છે.
($E$) ધાતુના ઓકસાઈડો સામાન્ય રીતે પ્રક્રુતિમાં એસિડિક અથવા તટસ્થ હોય છે.
નીચે આપેલા વિકલ્પોમાંથી સાથો જવાબ પસંદ કરો.
- 59ના માટે ઈલેકટ્રોન બંધુતા મુલ્ય (electron affinity value) ઋણ છે.View Solution
$A$. $\mathrm{Be} \rightarrow \mathrm{Be}^{-}$
$B$. $\mathrm{N} \rightarrow \mathrm{N}^{-}$
$C$. $\mathrm{O} \rightarrow \mathrm{O}^{2-}$
$D$. $\mathrm{Na} \rightarrow \mathrm{Na}^{-}$
$E$. $\mathrm{Al} \rightarrow \mathrm{Al}^{-}$
નીચે આપેલ વિકલ્પોમાંથી સૌથી બંધ બેસતો જવાબ પસંદ કરો.
- 60નીચે આપેલા તત્વો ની પ્રથમ આયનીકરણ એન્થાલ્પી મૂલ્યોનો સાયો કમ શોધો.:View Solution
$(A)$ $\mathrm{O}$ $(B)$ $\mathrm{N}$ $(C)$ Be $(D)$ $\mathrm{F}$ $(E)$ $B$
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 61નીચેના તત્વોમાંથી કેટલાક તત્વોનો સંખ્યા $CANNOT$ પ્રમાણો સાથે મેળ ખાતો મિલતો નથી તેનો આંકડો કેટલો છે:View Solution
$B, C, N, S, O, F, P, Al, Si$
- 62નીચે બે વિધાનો આપેલા છે -View Solution
વિધાન $I$ : $Na$ ની ધાત્વિક ત્રિજ્યા $1.86 \mathrm{~A}^{\circ}$ છે અને $\mathrm{Na}^{+}$ની આાયનીક ત્રિન્યા $1.86 \mathrm{~A}^{\circ}$ કરતા ઓછી છે.
વિધાન $II$ : આયનો તેમના આનુષગિક તત્વો કરતા કદ માં હંમેશા નાના હોય છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિક્લ્પોમાંથી સાયો જવાબ પસંદ કરો.
- 63નીચે બે વિધાનો આપેલા છે :View Solution
વિધાન ($I$) : ચૌક્કસ સંયોજનોમાં રહેલા તત્વની ઓક્સિડેશન અવસ્થા અણુમાં રહેલા અન્ય પરમાણુઓની ઈલેકટ્રોન પ્રાપ્તિ એન્થાલ્પી ને અનુરૂપ પરમાણુઓએ પ્રાપ્ત કરેલ વીજભાર છે.
વિધાન ($II$) : $p \pi-p \pi$ બંધ નું સર્જન (નિર્માણ) અન્ય આવર્ત ની તુલનામાં દ્રીતિય આવર્ત ના તત્વોમાં વધુ પ્રચલિત છે.
ઉપરના વિધાનોની સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચું બંધબેસતો જવાબ પસંદ કરીને લખો.
- 64નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : $\mathrm{Li}, \mathrm{Na}, \mathrm{F}$ અને Cl ની પ્રથમ આયનીકરણ એન્થાલ્પી મૂલ્યો નો સાચો ક્રમ $\mathrm{Na}<$ $\mathrm{Li}<\mathrm{Cl}<\mathrm{F}$ છે.
વિધાન $II$ : : $Li, Na, F$ અને $C1$ ના ઋણ ઇલેકટ્રોન પ્રાપ્તિ એન્થાલ્પી મૂલ્યો નો સાચો ક્રમ $\mathrm{Na}<\mathrm{Li}<\mathrm{F}<\mathrm{Cl}$ છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો જવાબ પસંદ કરો.
- 65View Solutionપ્રથમ આયનીકરણ ઉર્જા નો સાયો ક્રમ શોધો.
- 66સૂચિ $I$ સાથે સૂચિ $II$ ને જોડો.View Solution
સૂચિ-$I$ (તત્વો) સૂચિ-$II$(તેમના સંબંધિત સમૂહો માં ગુણધર્મો) $A$ $\mathrm{Cl}, \mathrm{S}$ $I$ સૌથી વધુ વિદ્યુતઋણતા સાથેના તત્વો $B$ $\mathrm{Ge}, \mathrm{As}$ $II$સૌથી વધુ (મીટ્રુ) પરમાણ્વીય કદ સાથેના તત્વો $C$ $\mathrm{Fr}, \mathrm{Ra}$ $III$તત્વો કે જે ધાતુઓ અને અધાતુઓ બંનેના ગુણધર્મો દર્શાવે $D$ $\mathrm{F}, \mathrm{O}$ $IV$ સૌથી વધુ (ઊંચી) ઋણ ઈલેકટ્રોન પ્રાપ્તિ અન્થાલ્પી સાથેના તત્વો નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો
- 67જો એક તત્વનું $IUPAC$ નામ $“Unununium"$ હોય તો તે તત્વ આવર્તકોષ્ટકના $n^{\text {th }}$ સમુહને (આભાસી છે). $n$ નું મુલ્ય__________છે.View Solution
- 68View Solutionતત્વ કે જે સૌથી વધારે પ્રથમ આયનીકરણ એન્થાલ્પી ધરાવે. છે તે શોધો.
- 69_____________ના વડે સમઈલેકટ્રોનીય સ્પીસીઝો ના કિસ્સામાં $\mathrm{F}^{-}, \mathrm{Ne}$ અને $\mathrm{Na}^{+}$ના કદ (આકાર) ને અસર થાય છે :View Solution
- 70નીચે આપેલ તત્વોની ઈલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પીનો યોગ્ય ક્રમ જણુાવો.View Solution
$A$. $\mathrm{Ar}$ $B$. $\mathrm{Br}$ $C. F$ $D$. $\mathrm{S}$
- 71નીચેના તત્વોને ધ્યાનમાં લો. સમૂહ. તો $A'$, $B'$, $C'$ અને $D'$ માટે યોગ્ય વિધાન શોધો ?View Solution
$A.$ પરમાણુ ત્રિજ્યાનો ક્રમ: $\mathrm{B}^{\prime}<\mathrm{A}^{\prime}<\mathrm{D}^{\prime}<\mathrm{C}^{\prime}$
$B.$ ધાત્વીય લક્ષગનો ક્રમ: $\mathrm{B}^{\prime}<\mathrm{A}^{\prime}<\mathrm{D}^{\prime}<\mathrm{C}^{\prime}$
$C.$ તત્વનાકદનો ક્રમ: $\mathrm{D}^{\prime}<\mathrm{C}^{\prime}<\mathrm{B}^{\prime}<\mathrm{A}^{\prime}$
$D.$ આયોનીક ત્રિજ્યાનો ક્રમ: $\mathrm{B}^{\prime+}<\mathrm{A}^{\prime}+<\mathrm{D}^{\prime}+<\mathrm{C}^{\prime}+$
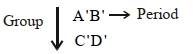
- 72નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન ($I$) : $p$ અને $d$-વિભાગ બંને પ્રકારના તત્ત્વો, ધાતુઓ અને અધાતુઓ ધરાવે છે.
વિધાન ($II$) : અધાતુઓની આયનીકરણ એન્થાલ્પી અને વિદ્યુતઋણુ ધાતુઓ કરતાં વધારે હોય છે.
ઉપરનાં વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી બંધબેસતો જવાબ પસંદ કરો.
- 73નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન ($I$) : આવર્તકોષ્ટકમાં તત્વોની $4 f$ અને $5 f$ - શ્રેણીઓને વર્ગીકરણના સિધ્ધાંતને સાચવવા માટે અલગ રીતે મૂકવામાં આવેલ છે.
વિધાન ($II$) : $s-$વિભાગના તત્વો પ્રકૃત્તિમાં શુદધ સ્વરૂપમાં મેળવી શકાય છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિક્પોમાંથી સૌથી બંધબેસતો જવાબ પસંદ કરો.
- 74નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $- I$ : આવર્ત દરમિયાન, તત્વોની રાસાયણિક પ્રતિક્રિયાત્મકતા સમૂહ $1$ થી સમૂહ $18$ માં ધીરે ધીરે વધે છે.
વિધાન $- II$ : સમૂહ $1$ તત્ત્વો દૂવારા (વડે) બનતા ઓક્સાઈડોની પ્રકૃતિ બેઝિક છે જ્યારે સમૂહ $17$ તત્ત્વોની એસિડીક હોય છે.
ઉપરના વિધાનોના સંદર્ભમાં નીચે આપેલા વિકલ્પો માંથી સાચો જવાબ પસંદ કરો.
- 75નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : ફલોરિન તે તેના સમુહમાં સૌથી વધુ ઋણ ઈલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પી ધરાવે છે.
વિધાન $II$ : ઓક્સિજન તે તેના સમુહમાં સૌથી ઋણ ઈલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પી ધરાવે છે.
ઉપરના વિધાનોના સંદર્ભાં નીચે આપેલા વિક્પોમાંથી સાચો જવાબ પસંદ કરો.
- 76નીચે બે વિધાનો આપેલા છે. એકને કથન $A$ વડે લેબલ કરેલ છે અને બીજને કારણ $R$ વડે લેબલ કરેલ છે.View Solution
કથન $A$ : આવર્ત દરમિયાન પ્રથમ આયનીકરણ એન્થાલ્પી ઘટે છે.
કારણ $R$ : આવર્ત દરમિયાન વધતો કેન્દ્રીય ભાર એ પરિરક્ષણ (શીલ્ડીંગ) પર અધિક પ્રભાવી (ભારે) હોય છે. ઉપર્યુક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિક્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 77$B, C, N, Li, Be, O$ અને $F$ તત્વો માટે, પ્રથમ આયનીકરણ એન્થાલ્પીનો સાચો ક્રમ શોધો.View Solution
- 78View Solutionઆપેલ તત્વોની ધાત્વીક પ્રકૃતિનો સાચો ક્રમ નીચે આપેલામાંથી કયો દર્શાવે છે.
- 79View Solutionઆપેલ તત્વો માટે વિદ્યુતઋણતાનો સાચો ક્રમ શોધો.
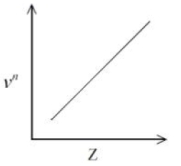
- 80તત્ત્વોના લાક્ષણિક $X-$કિરણ સ્પેક્ટ્રા નિયમિતતા દર્શાવે છે તેવું જોવા મળેલ છે. જ્યારે ઉત્સર્જિત $X-$કિરણોની આવૃત્તિથી ધાત (પાવર) “$n$” એટલે કે $v^n$ નો આલેખ (ગ્રાફ) પરમાણુક્રમાંક “$Z$” વિરુધ્ધ દોરવામાં આવે તો નીચે મુજબ આલેખ (ગ્રાફ) પ્રાપ્ત થાય છે.તો $n$નું મૂલ્ય શોધો.View Solution
- 81તત્વોની ઈલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પીઓ માટે $\Delta_{ eg } H$ તરીકે સૂચિત કરેલ છે.ખોટો વિકલ્પ શોધો.View Solution
- 82View Solutionધાત્વીક પ્રકૃતિનો સાચો ક્રમ શોધો.
- 83નીચે આપેલા વિધાનોમાંથી કયાં સાચાં નથી ?View Solution
$A$. $F$ ની ઈલેકટ્રોન પ્રાત્તિ એન્થાલ્પી એ $Cl$ ના કરતાં વધારે ઋણ છે.
$B$. આવર્તકોષ્ટકમાં સમૂહમાં આયનીકરણ એન્થાલ્પી ધટે છે.
$C$. પરમાણુનીવિદ્યુતઋણતા તેની સાથે જોડાયેલા પરમાણુઓ પર આધારિત છે.
$D$. ઊભયગુણી ઓકસાઈડોના ઉદાહરણો $Al _2 O _3$ અને $NO$ છે.
નીચે આપેલા વિકલ્પોમાંથી સૌથી બંધબેસતો જવાબ પસંદ કરો.
- 84સૂચિ$-I$ ને સૂચિ$-II$ સાથે જોડો.View Solution
સૂચિ $-I$ (પરમાણું ક્રમાંક) સૂચિ $-II$ (આવર્તકોષ્ટકનો વિભાગ) $A$ $37$ $I$ $p-$વિભાગ $B$ $78$ $II$ $d-$વિભાગ $C$ $52$ $III$ $f-$વિભાગ $D$ $65$ $IV$ $s-$વિભાગ બિચે આપેલા વિકલ્પોમાથી સાચો જવાબ પસંદ કરો.
- 85હેન્રી મોસલી તત્વોના લાક્ષણિક $X-$કિરણ વર્ણપટનો અભ્યાસ કર્યો આલેખ કે જે તેના અવલોકનની સાચી રજૂઆત (દર્શાવે) છે તે.(આપેલ $v =$ ઉત્સર્જિત $X-$કિરણની આવૃતિ)View Solution
- 86ની વચ્ચે ઇલેકટ્રોન પ્રાપ્તિ એન્થાલ્પીઓ વચ્યે નો તફાવત મહત્તમ થશે તે $.......$View Solution
- 87નીચે બે વિધાનો આપેલા છે. એક ને કથન $A$ વડે લેબલ કરેલ છે. અને બીજાને કારણ $R$ વડે લેબલ કરેલ છે.View Solution
કથન $A :$ $3d$ શ્રેણી તત્ત્વોની પ્રથમ આયનીકરણ એન્થાલ્પી એ સમૂહ $2$ તત્વોના કરતાં વધારે હોય છે.
કારણ $R :$ તત્વોની $3d$ શ્રેણીઆોમાં $d-$કક્ષકોનું ક્રમાનુસાર ભરાય છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી વધુ બંધ બેસતો જવાબ પસંદ કરો.
- 88$A, B, C, D$ ચાર તત્વોની સૌથી બહારની ઈલેક્ટ્રોન સંરચનાઓ નીચે આપેલ છે.View Solution
$3 s^{2}$; $3 s^{2} 3 p^{1}$; $3 s ^{2} 3 p ^{3}$; $3 s^{2} 3 p^{4}$
તો તેમના માટે પ્રથમ આયનીકરણ એન્થાલ્પીનો સાચો ક્રમ શોધો.
- 89$Be, B, N$ અને $O$ ની પ્રથમ આયનીકરણ એન્થાલ્પીઓ ક્રમને અનુસરે છે તે...View Solution
- 90એક તત્વ જેનું બાહ્ય ઈલેકટ્રોનીય સંરચના $[Rn] \,5 f ^{14} 6 d ^1 7 s ^2$ છે. તો $IUPAC$ નામકરણ મુજબ તે $....$View Solution
- 91View Solutionઘનતાનો સાચો ક્રમ કયો છે?
- 92તત્વ $"E"$ આવર્ત કોષ્ટકના આવર્ત $4$ અને સમુહ $16$ ને સંલગ્ન છે. તત્વ કે જેની સંયોજકતા કોશ ઈલેકટ્રોન સંરચના સમુહમાં $"E"$ ની તરત જ ઉપર છે તે શોધો.View Solution
- 93View Solutionનીચે આપેલા પૈકી બેઝિક ઓક્સાઈડ શોધો.
- 94નીચે બે વિધાનો આપેલા છે. એકને વિધાન $(A)$ તરીકે લેબલ કરેલ છે અને બીજા ને કારણ $(R)$ તરીકે લેબલ કરેલ છે.View Solution
વિધાન $(A)$ :$O^{2-}$ અને $Mg ^{2+}$ ની આયનિક ત્રિજ્યાઓ સમાન છે.
કારણ $(R)$ : બંને $O ^{2-}$ અને $Mg ^{2+}$ સમઈલેક્ટ્રોનીય સ્પીસિઝો છે.
ઉપરોક્ત વિધાનોના સંંદર્ભે, નીચે આપેલા વિકલ્પમાંથી યોગ્ય ઉત્તરની પસંદગી કરો.
- 95નીચે બે વિધાનો આપેલા છે. જે કથન $(A)$ અને કારણ $(R)$ તરીકે નિર્દેશીત કરેલા છે.View Solution
કથન $A:$ ઓક્સીજનની પ્રથમ આયનિકરણ એન્થાલ્પી નાઈટ્રોજન કરતા ઓછી છે.
કારણ $R:$ $2p$ કક્ષકમાં રહેલા ઓકિસજનના ચાર ઈલેકટ્રોન વધુ ઈલેક્ટ્રોન-ઈલેકટ્રોન અપાકર્ષણ અનુભવે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 96સૂચી $- I$ સાથે સૂચી $- II$ ને જોડોView Solution
સૂચી $- I$ ઓક્સાઈડ
સૂચી $- II$ (પ્રકૃતિ)
$(A)$ $Cl _{2} O _{7}$ $(I)$ ઉભયગુણી $(B)$ $Na _{2} O$ $(II)$ બેઝિક $(C)$ $Al _{2} O _{3}$ $(III)$ તટસ્થ $(D)$ $N _{2} O$ $(IV)$ એસિડીક નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો
- 97$Cl, F, Te$ અને $Po$ ની ઈલેકટ્રોન પ્રાતિ એન્થાલ્પીઓનો સાચો ક્રમ શોધો.View Solution
- 98$Na , Mg$ અને $Si$ ની પ્રથમ આયનીકરણ એન્થાલ્પી અનુક્રમે $496, 737$ અને $786 \,kJ / mol$ છે. તો $Al$ ની પ્રથમ આયનીકરણ એન્થાલ્પી ( $\left.kJ\, mol ^{-1}\right)$ માં શોઘો.View Solution
- 99View Solutionઆયનિક ત્રિજ્યાઓનો સાચો ચઢતો ક્રમ શોધો.
- 100View Solutionખોટું વિધાન શોધો.