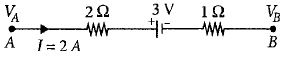Series :
\(R_{e q}=R_1+R_2\)
\(2 R\left(1+\alpha_{e q} \Delta \theta\right)=R\left(1+\alpha_1 \Delta \theta\right)+R\left(1+\alpha_2 \Delta \theta\right)\)
\(2 R\left(1+\alpha_{\mathrm{eq}} \Delta \theta\right)=2 R+\left(\alpha_1+\alpha_2\right) R \Delta \theta\)
\(\alpha_{\mathrm{eq}}=\frac{\alpha_1+\alpha_2}{2}\)
Parallel :
\(\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}\)
\(\frac{1}{\frac{R}{2}\left(1+\alpha_{e q} \Delta \theta\right)}=\frac{1}{R\left(1+\alpha_1 \Delta \theta\right)}+\frac{1}{R\left(1+\alpha_2 \Delta \theta\right)}\)
\(\frac{2}{1+\alpha_{\mathrm{eq}} \Delta \theta}=\frac{1}{1+\alpha_1 \Delta \theta}+\frac{1}{1+\alpha_2 \Delta \theta}\)
\(\frac{2}{1+\alpha_{\mathrm{eq}} \Delta \theta}=\frac{1+\alpha_2 \Delta \theta+1+\alpha_1 \Delta \theta}{\left(1+\alpha_1 \Delta \theta\right)\left(1+\alpha_2 \Delta \theta\right)}\)
\(2\left[\left(1+\alpha_1 \Delta \theta\right)\left(1+\alpha_2 \Delta \theta\right)\right]\)
\(=\left[2+\left(\alpha_1+\alpha_{22}\right) \Delta \theta\right]\left[1+\alpha_{\mathrm{eq}} \Delta \theta\right]\)
\(2\left[1+\alpha_1 \Delta \theta+\alpha_2 \Delta \theta+\alpha_1 \alpha_2 \Delta \theta\right]\)
\(=2+2 \alpha_{\mathrm{eq}} \Delta \theta+\left(\alpha_1+\alpha_{22}\right) \Delta \theta+\alpha_{\mathrm{eq}}\left(\alpha_1+\alpha_2\right) \Delta \theta^2\)
Neglecting small terms
\(2+2\left(\alpha_1+\alpha_2\right) \Delta \theta=2+2 \alpha_{\mathrm{eq}} \Delta \theta+\left(\alpha_1+\alpha_2\right) \Delta \theta\)
\(\left(\alpha_1+\alpha_2\right) \Delta \theta=2 \alpha_{\mathrm{eq}} \Delta \theta\)
\(\alpha_{\mathrm{eq}}=\frac{\alpha_1+\alpha_2}{2}\)
Download our appand get started for free
Similar Questions
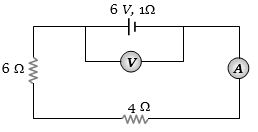
- 1View Solutionઆપેલ પરિપથમાં એમિટર અને વોલ્ટમીટરનું અવલોકન કેટલું હશે?
- 2$10$ બલ્બને $220\,V$ સપ્લાય સાથે શ્નેણીમાં લગાવ્યા છે.એક બલ્બ ઊડી જવાથી બાકીના બલ્બ શ્નેણીમાં લગાવતા પ્રકાશની તીવ્રતા...View Solution
- 3પોટેન્શિયોમીટર દ્વારા બે કોષને શ્રેણીમાં સહાયકમાં જોડતાં તટસ્થ બિંદુ $6\, m$ અને બે કોષને શ્રેણીમાં વિરોધકમાં જોડતાં તટસ્થ બિંદુ $2\, m $ અંતરે મળે છે.તો બંને કોષનાં $emf$ નો ગુણોત્તર કેટલો થાય?View Solution
- 4ચોરસની બાજુઓ $AB, BC, CD $ અને $ DA $ પર અનુક્રમે $10\, \Omega, 5\, \Omega, 7\, \Omega$ અને $ 3 \,\Omega $ અવરોધ જોડવામાં આવે છે,વિકીર્ણ $ AC$ પર $10 \,\Omega$ અવરોઘ જોડવામાં આવે તો $A $ & $ B $ ની વચ્ચે સમતુલ્ય અવરોધ કેટલા ............... $\Omega$ થાય?View Solution
- 5ત્રણ કોપરના તારની લંબાઇ અને આડછેદ $(l,\,A),\,(2l,\,A/2)$ અને $(l/2,\, 2A)$ છે.તો અવરોધ લઘુતમView Solution
- 6બે $220\; V , 100 \;W$ ના બલ્બને પ્રથમ શ્રેણીમાં અને પછી સમાંતરમાં જોડવામાં આવે છે. દરેક વખતે જ્યારે સંયોજન $220 \;V \;AC$ સપ્લાય સાથે જોડવામાં આવે છે. દરેક કિસ્સામાં અનુક્રમે સંયોજન દ્વારા ખેંચાતો પાવર કેટલો હશે?View Solution
- 7કોષના આંતરિક અવરોધ શોધવા માટે પોટેન્શિયોમીટરમાં જ્યારે કોષ ખુલ્લા પરિપથમાં (open circuit) હોય ત્યારે તટસ્થ બિંદુ માટે તારની લંબાઈ $\ell $ મળે છે. હવે કોષને $R$ અવરોધ વડે શોર્ટ સર્કિટ કરવામાં આવે છે. જો $R$ નું મૂલ્ય કોષના આંતરિક અવરોધના મૂલ્ય જેટલું હોય તો પોટેન્શિયોમીટરમાં તટસ્થ બિંદુ માટે તારની લંબાઈ કેટલી મળશે?View Solution
- 8$1.0\, m$ લંબાઇ અને $0.6\, cm$ વ્યાસ ધરાવતા તારનો અવરોધ $3.0 × 10^{-3}\, Ω$ છે.સમાન દ્રવ્યમાંથી બનાવેલ $2.0\, cm$ વ્યાસ અને $1.0\, mm$ જાડાઇ ધરાવતી તકતી વચ્ચેનો અવરોધ કેટલો થાય?View Solution
- 9કારની એક સંગ્રાહક બૅટરીનું $emf$ $12\, V$ છે. જો બૅટરીનો આંતરિક અવરોધ $0.4\; \Omega$ હોય તો બૅટરીમાંથી કેટલો મહત્તમ પ્રવાહખેંચી શકાય?View Solution
- 10નીચે આપેલી આકૃતિમાં $A$ અને $B$ બિંદુઓ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત $(V_A-V_B)$ .............. $V$ શોધો.View Solution