$0.1\, kg$ દળના બ્લોકને $640\, Nm^{-1}$ બળ અચળાંક ધરાવતી સ્પ્રિંગ સાથે જોડેલ છે. જે $10^{-2}\, kg\,s^{-1}$ ના અવમંદિત અચળાંક ધરાવતા માધ્યમમાં દોલનો કરે છે.તંત્ર સમાન રીતે ઉર્જા ગુમાવે છે.તંત્રની યાંત્રિક ઉર્જા શરૂઆત કરતાં અડધી થતાં કેટલો સમય($s$ માં) લાગશે?
JEE MAIN 2017, Diffcult
b
Since system dissipates its energy gradually, and hence amplitude will also decreases with time according to
Since system dissipates its energy gradually, and hence amplitude will also decreases with time according to
\(a=a_{0} \mathrm{e}^{-\mathrm{bt/m}}\) \(...(i)\)
Energy of vibration drop to half of its in itial value \(\left(\mathrm{E}_{0}\right),\) as \(\mathrm{E} \propto \mathrm{a}^{2} \Rightarrow \mathrm{a} \propto \sqrt{\mathrm{E}}\)
\(a=\frac{a_{0}}{\sqrt{2}} \Rightarrow \frac{b t}{m}=\frac{10^{-2} t}{0.1}=\frac{t}{10}\)
From \(eq^n(i),\)
\(\frac{a_{0}}{\sqrt{2}}=a_{0} e^{-t / 10}\)
\(\frac{1}{\sqrt{2}}=e^{-t / 10}\) or \(\sqrt{2}=e^{\frac{t}{10}}\)
\(\ln \sqrt{2}=\frac{t}{10} \quad \therefore t=3.5\) seconds
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસરળ આવર્તગતિ કરતાં સાદા લોલક માટે આવર્તકાળ વિરુઘ્ઘ લંબાઇનો આલેખ કેવો બને?
- 2એક કણ $A$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે.કણ જયારે તેની સરેરાશ અવસ્થાની $\frac{{2A}}{3}$ જેટલા અંતરે હોય છે,ત્યારે અચાનક તેની ઝડપ ત્રણ ગણી કરી દેવામાં આવે છે.કણનો નવો કંપવિસ્તાર છે:View Solution
- 3$l_{A}$ અને $l_{B}$ લંબાઈ ધરાવતી બે સ્પ્રિંગના છેડે અનુક્રમે $M_{A}$ અને $M_{B}$ દળ લટકવેલા છે. જો તેમના દોલનોની આવૃતિ વચ્ચેનો સંબંધ $f_{A}=2 f_{B}$ હોય તો .....View Solution
- 4$T$ આવર્તકાળ સાથે એક કણ સરળ આવર્ત ગતિ કરે છે. જો તેની કુલ યાંત્રિક ઉર્જાનો આવર્તકાળ $T^{\prime}$ હોય તો $\frac{T^{\prime}}{T}$ તો કેટલો થશે?View Solution
- 5બળપ્રેરિત દોલનોમાં કણનો કંપવિસ્તાર બળની $\omega_{1}$ આવૃતિ માટે મહત્તમ, જ્યારે બળની $\omega_{2}$ આવૃતિ માટે ઉર્જા મહત્તમ હોય, તોView Solution
- 6$5\, {kg}$ દળને સ્પ્રિંગ સાથે જોડેલ છે. આ તંત્ર દ્વારા થતી સરળ આવર્તગતિની સ્થિતિઊર્જાનો ગ્રાફ આકૃતિમાં દર્શાવેલ છે. $4\, {m}$ લંબાઈના સાદા લોલકનો આવર્તકાળ સ્પ્રિંગતંત્રના આવર્તકાળ જેટલો જ છે. જ્યાં આ પ્રયોગ કરવામાં આવેલ છે તે ગ્રહ પર ગુરુત્વપ્રવેગનું મૂલ્ય (${m} / {s}^{2}$ માં) કેટલું હશે?View Solution
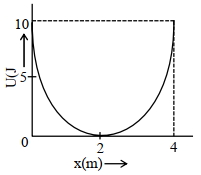
- 7આપેલ સમયે સાદા આવર્ત લોલકના સ્થાનાંતરનું મૂલ્ય $y = A \cos \left(30^{\circ}\right)$ વડે આપવામાં આવે છે. જો કંપવિસ્તાર $40\,cm$ હોય અને આ સમયે ગતિઊર્જા $200\,J$ હોય, તો બળ અચળાંકનું મૂલ્ય $1.0 \times 10^x Nm ^{-1}$ છે. $x$ નું મૂલ્ય ....... થશે.View Solution
- 8$1\, s$ આવર્તકાળ ધરાવતું લોલક આવામંદનને કારણે ઉર્જા ગુમાવે છે.એક સમયે તેની ઉર્જા $45\, J$ છે જો $15 $ દોલનો પછી તેની ઉર્જા $15\, J$ થતી હોય તો અવમંદનનો અચળાંક (damping constant$=\frac bm$) ($s^{-1}$ માં) કેટલો થાય?View Solution
- 9સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $ x = 12\sin \omega t - 16{\sin ^3}\omega t $ હોય,તો મહત્તમ પ્રવેગ કેટલો થાય?View Solution
- 10સરખી સીધી રેખામાં બે કણ $P$ અને $Q$ એ સમાન કંપનવિસ્તાર $a$, સમાન આવૃત્તિ $f$ સાથે ગતિ કરે છે. બંને કણ વચ્ચેનું મહત્તમ અંતર $\sqrt{2}$ છે. કણના પ્રારંભિક કળા વચ્ચેનો તફાવત $.................$View Solution
